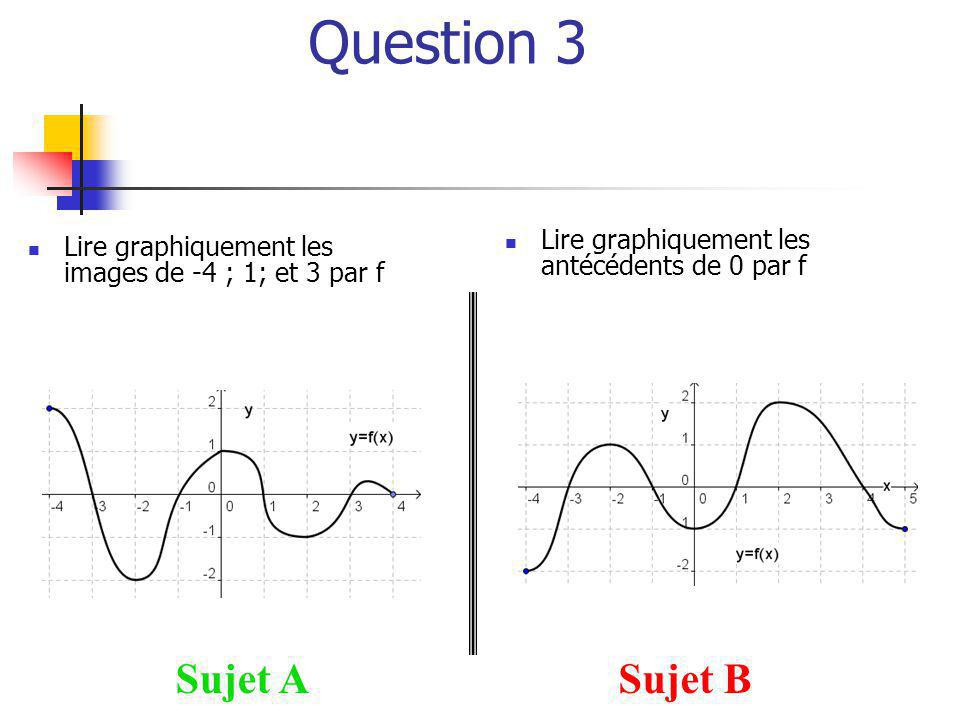
Solution f(x)=0 ⇔ x=1/2;Soit la fonction f définie sur ℝ par f(x) = x 2 et 𝒞 f sa courbe représentative À l'aide du taux de variation, on a calculé f'(1) = 2 Exemple 2 La tangente T a pour de coefficient directeur 2 et passe par le point A(1 ;Wwwmathsenlignecom XERCICES FONCTIONS NUMERIQUES D'UNE VARIABLE REELLE E 9A C ORRIGE – NOTRE DAME DE LA MERCI MONTPELLIER EXERCICE 9A1 Les courbes C f, C g, C h et C k qui représentent les fonctions f, g, h et k j a Résoudre graphiquement les équations f (x) = 3 si x = 1 ou x = 2 g(x) = 2 si x = 3 ou x = 3 h(x) = 3 si x = 3 k(x) = 4 si x = 4 ou x = 1

Comment Determiner Graphiquement La Valeur D Un Nombre Derive D Une Fonction Youtube
Respudre graphiquement f(x) 0
Respudre graphiquement f(x) 0-Graph xy=0 Solve for Tap for more steps Subtract from both sides of the equation Multiply each term in by Tap for more steps Multiply each term in by Multiply Find the xintercept Tap for more steps To find the xintercept (s), substitute in for and solve for Rewrite the equation as xintercept (s) in point formChapitre I G en eralit es sur les fonctions Classe de Premi ere S 3 a) Tracer une repr esen tation graphique des fonctions f et g dont voici le tableau de variation x f(x) −4 −1 0 3 5 0 −2 1 0 2 −2 0 1 3 0 2 3 −2 x g(x) b) R esoudre graphiquement l' equation f(x)=0



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora
Exercice de maths corrigés2nde Résolution d'équations et d'inéquations (f(x)=0, f(x)F x sin 5x 2 et f x sin x et f x sin2xcos3x et f x 3 tan 3x et f x x 3sinx 2 4 2 f x x et f x x et f x x 7x 12 et f x x 7x 12 2 2 3 Etudier la dérivabilité de la fonction f au point x 0 1 a x1 0 fxavec x x 2x 12 x1 f 0 1 ° ® ° ¯ b x0 0 avec ° x 1 1 x fx x f 0 0 ° ® ¯ c avec 3 2 f x 7x 1 , x 0 3x 1 f x , x 0 x1 °
Http//jaicompriscom/lycee/math/fonction/derivation/derivationcalculphp savoir lire le nombre dérivée f'(3) et pas confondre avec f(3) savoir résoudre gRésoudre graphiquement une équation du type \(f(x)=k\) revient à chercher les antécédents éventuels de \(k\) par \(f\) Cette méthode a été vue au paragraphe précédent Précédent;7 7) Déterminer graphiquement le maximum de f Pour quelle valeur de x estil atteint ?
Le maximum de f vaut 4,5 Il est atteint pour x = 5 8) Compléter le tableau de variations de la fonction f x – 5 – 4 1,5 3 5 7Soit f x = ax2 bx c avec a, b, c réels et a 0 a Lire graphiquement le signe de f x et celui de a pour chacune des six courbes représentatives de f données dans la question 3 de l'activité 3 b Si le discriminant D de f x est négatif ou nul, quelle conjecture peuton émettreRésoudre algébriquement l'équation f(x)=g(x) × Après avoir cliqué sur "Répondre" vous serez invité à vous connecter pour que votre message soit publié × Attention, ce sujet est très ancien
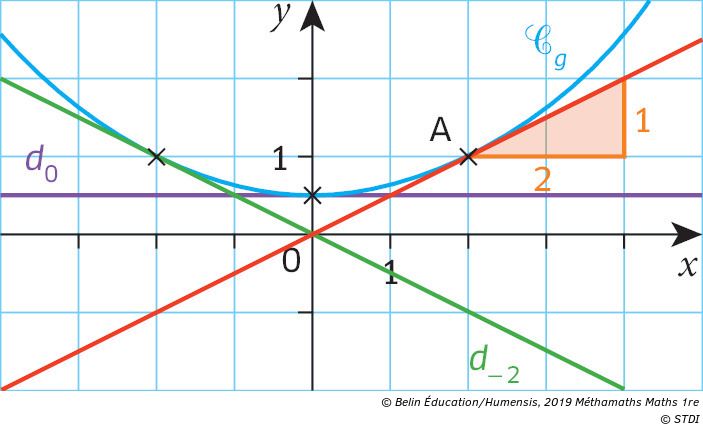



Cours 2 Tangentes A Une Courbe Et Fonction Derivee Manuel Numerique Max Belin
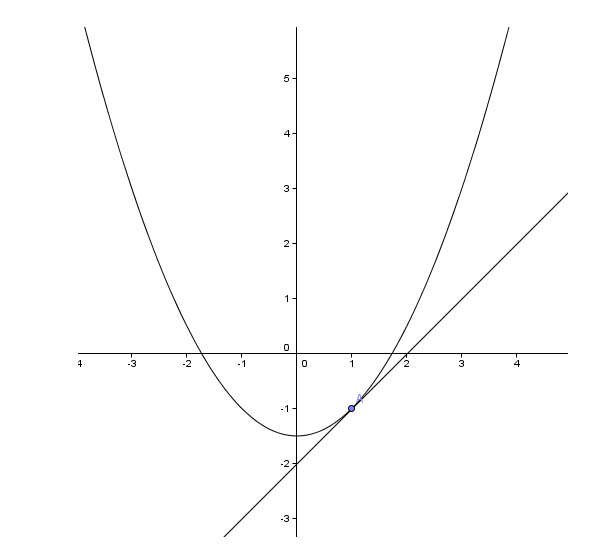



Determiner Graphiquement F X Forum Mathematiques
Déterminer graphiquement l'expression de la fonction affine dont on a tracé la courbe j = –0,5 3 f (x) = x 2,5 f (x) = 0,515 3 Résoudre graphiquement une équation Soit f et g deux fonctions défi nies sur une partie D de ˚ et (˚) et (˚') leurs courbes représentatives Soit k un nombre réel • Résoudre graphiquement dans D l'équation f(x)˚=˚k revient à déterminer dans D les antécédents de k par f, c'estàdire les abscisses des points de la courbe (˚) d'ordonnée égale à kA onesided limit is the value the function approaches as the xvalues approach the limit from *one side only* For example, f (x)=x/x returns 1 for negative numbers, 1 for positive numbers, and isn't defined for 0 The onesided *right* limit of f at x=0 is 1, and the onesided *left* limit at x=0 is 1 Created by Sal Khan This is the
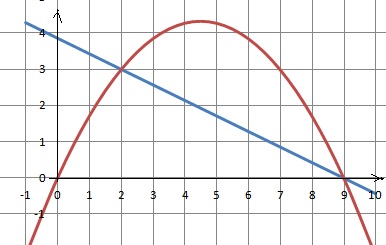



Mathematiques Controle Continu Premiere Technologique 01
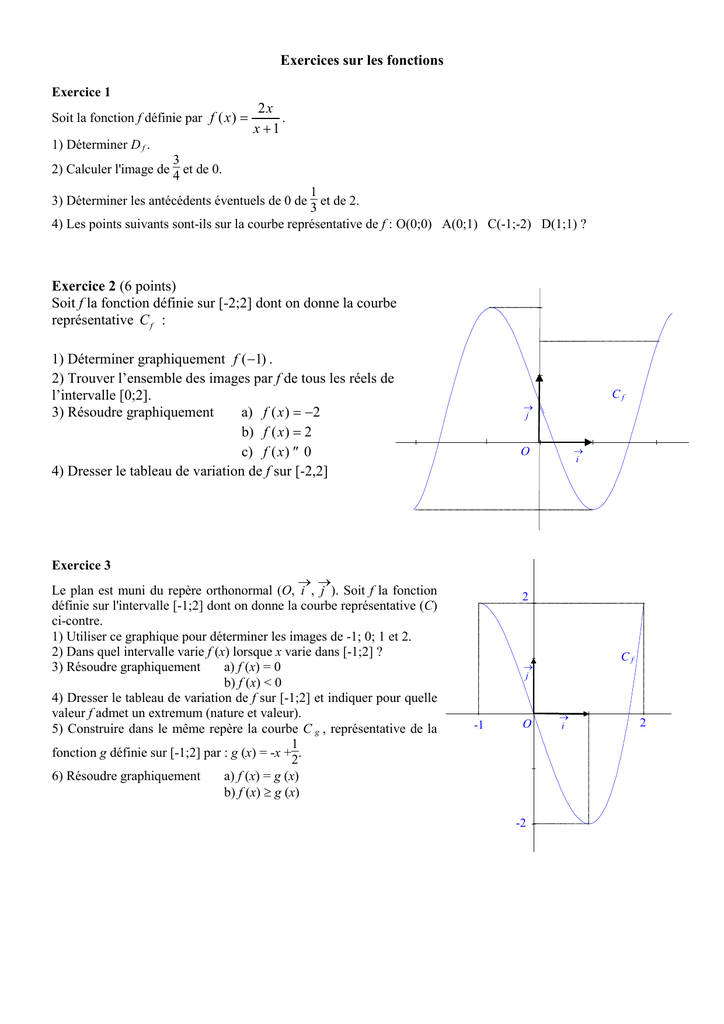



Exercices Sur Les Fonctions X X 2 1 Exercice 2 6 Points Soit F
Algebra Graph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope andRésoudre graphiquement l'inéquation h(x) ⩾ 2 sur l'intervalle −3 ;Nombres De Solutions D Une Equation 1 Resoudre Graphiquement A F X 3 B F X 5 C F X 0 D F X Ppt Download For more information and source, see on this link https




Mathematique En Terminale Bac Pro Resoudre Graphiquement Une Equation De La Forme F X 0




2 Resolution Graphique D Equations Du Type F X K Et F X G X Lelivrescolaire Fr
5) Déterminer graphiquement f (0) = 1,5 6) Résoudre graphiquement l'inéquation f (x) < 3 S = – 5 ;Résoudre graphiquement f(x)=0 ;f(x)≥ 0 g(x)=0 ;g(x)≥ 0 ;C Représentation graphique d'un trinôme du second degré Théorème La courbe représentative d'une fonction du type f(x)=ax2bxc (avec a≠0) est une parabole Cette parabole est tournée vers le haut si a>0 et elle est tournée vers le bas si a



Http Ressources Sesamath Net Coll Send File Php File Cahlp Valide Cslp1 15 P4 Pdf
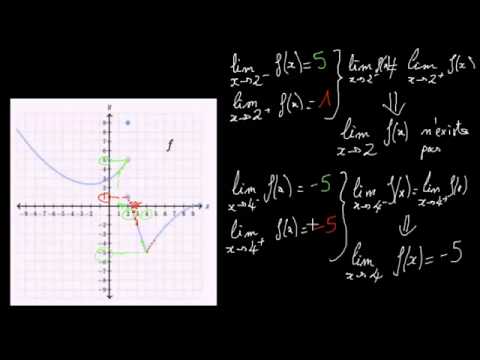



Determiner Graphiquement Une Limite A Gauche Ou Une Limite A Droite En Un Point Video Khan Academy
J), la représentation graphique de la fonction affine x → ax b est la droite d'équation y = ax b a est le coefficient directeur de la droite et b est son ordonnée à l'origine Soit la fonction affine f définie par f ( x ) = 2 x – 1X définie par f x x x 2 2 ① a Déterminer D f l'ensemble de définition de la fonction f b Calculer lim x fx f ② Etudier la dérivabilité de f en 0 à droite et interpréter le résultat graphiquement ③ a Calculer fx ' pour tout xD f ^0` b Etudier les variations de f ④ apour tout Calculer fx''The limit as x>0 from the right of sqrt (x) is 0 However, limit as x>0 from the left of sqrt (x) is does not exist, and since the limit from the left does NOT equal the limit from the right, then the limit from both sides does not exist Conversely, the limit as x>1 from the right of sqrt (x) is 1 And, limit as x>1 from the left of sqrt



Representer Graphiquement Une Suite Un F N Et Un 1 F Un




2 Resolution Graphique D Equations Du Type F X K Et F X G X Lelivrescolaire Fr
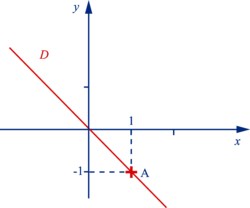
Soit la fonction linéaire f définie par f(x) = – x • Sa représentation graphique est une droite D qui passe par l'origine • Pour construire D , il suffit de déterminer les coordonnées d' un autre de ses points, c'estàdire un nombre et son image par fCe qu'il faut bien comprendre c'est que le nombre dérivé f' d'une fonction f c'est le coefficient directeur de la tangente à la courbe représentative de cette fonctionDans le cas où f'(x) = 0, celaNombres De Solutions D Une Equation 1 Resoudre Graphiquement A F X 3 B F X 5 C F X 0 D F X Ppt Download For more information and source, see on this link https



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora
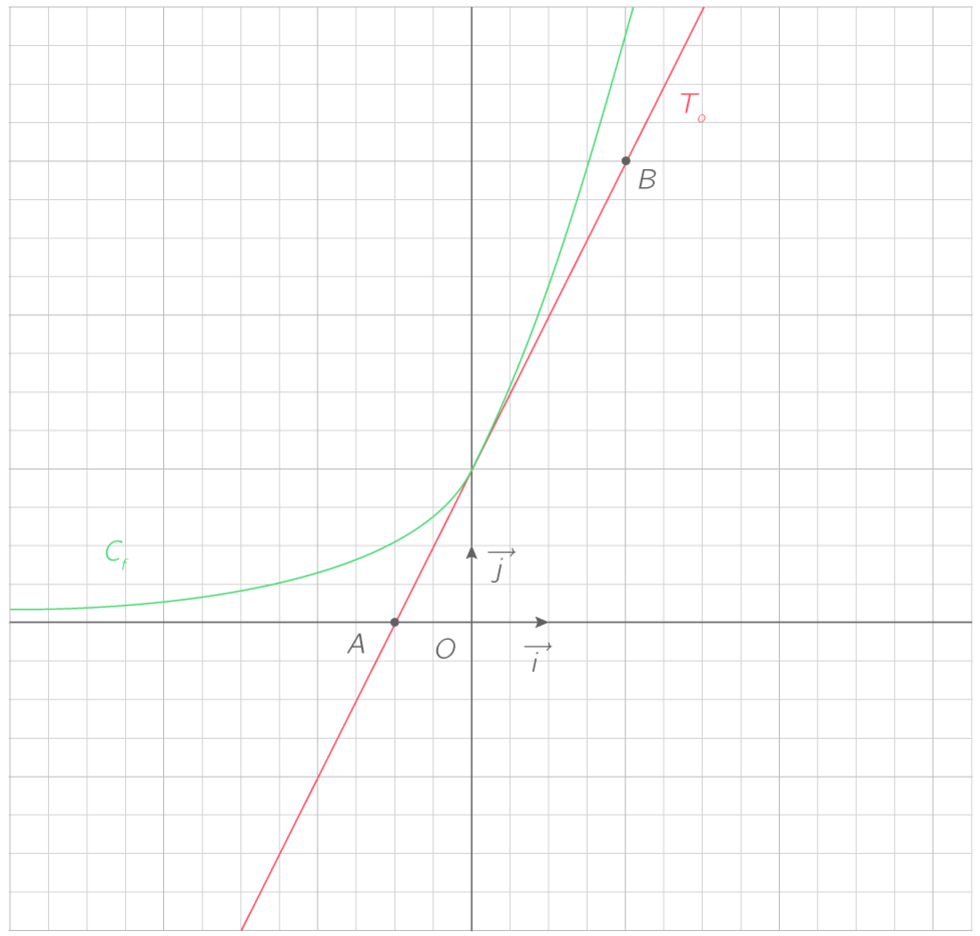



Determiner Graphiquement La Valeur De F A Cours Terminale S
5, c'est trouver toutes les solutions appartenant à cet intervalle Pour savoir si un nombre x est solution, on regarde si le point de la courbe d'abscisse x a une ordonnée h(x) supérieure ou égale à 2Autrement dit, on regarde si ce point est audessus de la droite d formée de tous les points d'ordonnée 2 ou sRésoudre graphiquement dans l'équation g(x) f(x) 5résoudre graphiquement dans l'inéquation t g(x) 0 6résoudre graphiquement dans l'inéquation t g(x) f(x) figure 1 EXERCICE 3 10 points Le plan est rapporté a un repère orthonormé O , OI , OJ EFG est un triangle et K le milieu de > @ FG > @ GH est un hauteur au triangleUne fonction affine est représentée graphiquement par une droite qui n'est pas parallèle à l'axe des ordonnées Cas particuliers Si b = 0, f(x) = ax, f est une fonction linéaire et la représentation graphique est une droite passant par l'origine O Si a = 0, f(x) = b, f est constante et la droite est parallèle à l'axe des




Bonjour J Aimerais De L Aide Pour Ces Exercices S Il Vous Plait Merci 1 A Resoudre Nosdevoirs Fr



A Propos
Déterminer l'ensemble des solutions de f (x) > 0 noncé On considère les fonctions affinesf et g définies sur R par f (x) = —3x9 et g(x)= 2x8 1 Construire le tableau de signes de chacune des fonctionsf et g Résoudre graphiquement les equations et suivantes 2 Soit la fonction h définie sur —5 2 par = 2x 3 À raideA) f(x) = 0 b) f(x) = g(x) c) f(x) ≥ g(x) 3) Interpréter graphiquement les résultats de la question 2 Approfondissement 6 Fonction affine par morceaux ? Résoudre graphiquement f'(x)=0 0 /5 (0 votes) Comment résoudre f'(x)=0 lorsqu'on a la représentation graphique de la fonction?




Etablissement Al Fetna Home Facebook



Mathematiques Concours Externe Tspei 19
Soit Un une suite et M un réel tel que Un = M pour tout n, on dit que Un est _1°) Résoudre l'inéquation f x 0 (1) a) graphiquement b) par le calcul 2°) Déterminer la fonction affine g qui est représentée graphiquement par la droite D 3°) Résoudre l'inéquation f x g x (2) a) graphiquement b) par le calculDéfinition Une fonction est dite « affine par morceaux » lorsqu'elle est définie sur des intervalles de ℝ par différentes fonctions affines



Http Qotsaupload Free Fr 1sti Derivation Eva01 Pdf




Comment Representer Graphiquement Les Termes D Une Suite Recurrente Les Suites Numeriques Tes J Ai En Maths
Dans un plan muni d'un repère (O ; Niveau 3 Quelle est la dérivée de la fonction f (x)=2x²3 ?From the graph of f(x), draw a graph of f ' (x) We can see that f starts out with a positive slope (derivative), then has a slope (derivative) of zero, then has a negative slope (derivative) This means the derivative will start out positive, approach 0, and then become negative Be Careful Label your graphs f or f ' appropriately When we're graphing both functions and their derivatives




Resoudre Graphiquement Une Inequation Du Type F X K 2nde Exercice Mathematiques Kartable




What Is The Meaning Of Second Derivative Mathematics Stack Exchange
résoudre f(x)=g(x) soit \( (fg)(x)=0 \) On recopie, et on range \( x^22x3 2x7 =0 \) soit \( x^2 4x 4 =0 \) tu trouve le discriminent, et tu calcules les éventuelles racines Ensuite tu vérifie qu'elles sont cohérentes avec le problème initiale edit Comme l'a dit holomos, il y a surement une belle mise en facteur à faire1) Déterminer graphiquement f'(−2) et f'(0)3,5;3,5 donc f 0 3,5 , f 2 3,5 , 3,5 3,5 Les solutions de l'équation f(x) = 3,5 sont x = 0 , x = 2 , x = –3,5 Résoudre l'équation f(x) = 0 graphiquement deux solutions a = 4 et x = 7 (car f 40 et f
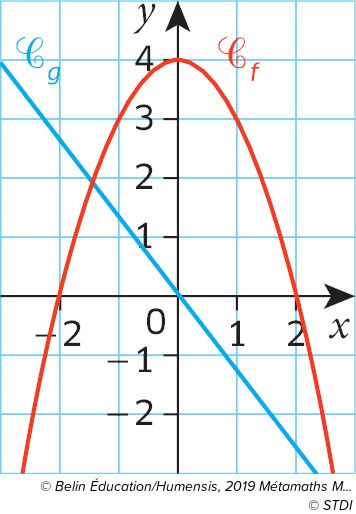



Entrainement Resoudre Graphiquement Une Equation F X G X Manuel Numerique Max Belin




Resolutions Graphiques Maxicours
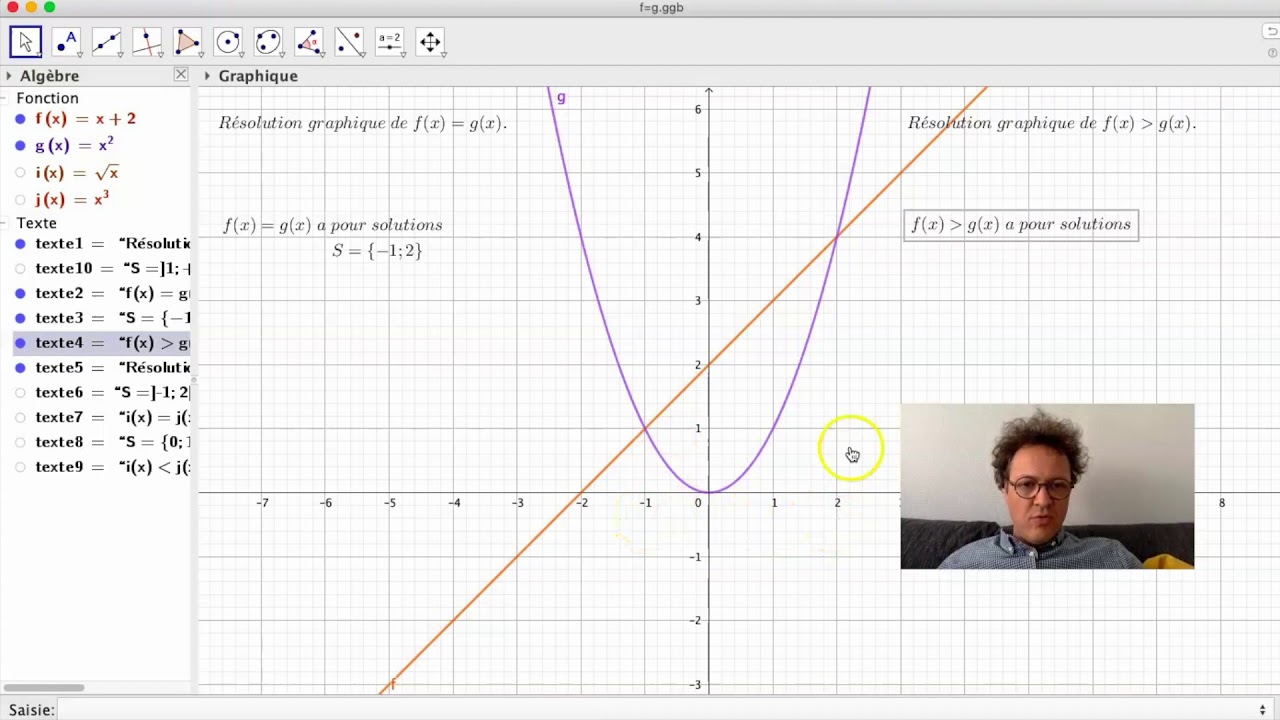
Notion de fonction Tableau et courbe Résolution graphique d'équations Résolution graphique de f(x)=k Résolution graphique de f(x)=g(xLes solutions de l'équation f(x) = g(x) sont les abscisses des points d'intersection des deux courbes Cf et Cg Les solutions de l'équation f(x) = g(x) sont donc S = {x1;x2} Résolution graphique des inéquations 1er cas 1er cas inéquations du type f(x) ≥ k où k appartient à ℜFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 / f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domain



2
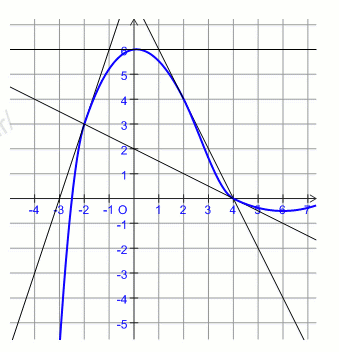



Resoudre F X Sur Une Representation Graphique Forum Mathematiques
H(x)=0 et h(x)≥ 0 5)a)Déterminer f(0) en déduire la valeur de a b) Déterminer g (1) en déduire la valeur de b c)Déterminer h(0) en déduire la valeur de c 6)a) Résoudre graphiquement l'équation g(x)=x b)Retrouver ce résultat par le calcul Lycées ThelèpteRésoudre graphiquement l'inéquation f(x)F(x) = 2x 3 Remarque, pour faciliter la compréhension de la représentation graphique, on peut remplacer f(x) par y Ce qui donne ici y = 2x 3 Soit A et B, deux points de la droite représentative de la fonction f(x) = 2x 3 que nous nommerons D1 Libre à nous de choisir les deux valeurs de x pour les deux points Nous prendrons ici 0 et 1



Fonction Definition Image Antecedent
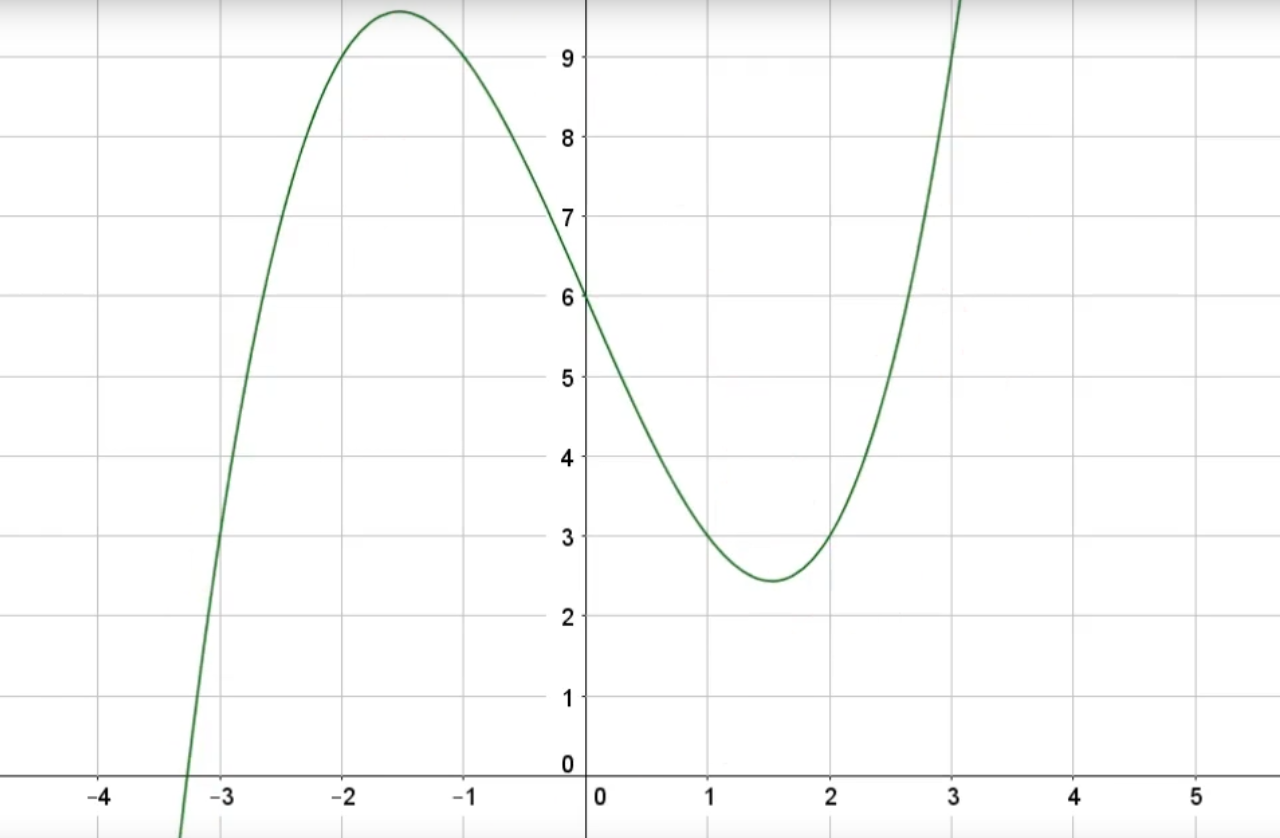



2eme Notion De Fonction
Graphiquement,l'équation f'(x)=0 admet une solution qui est l'abscisse des points d'intersections de la tangente avec l'axe des abscisses On obtient donc pour solutions un nombre0 Deuxième partieLet's say that f of X is equal to the absolute value of X minus 3 over X minus 3 and what I'm curious about is the limit of f of X the limit of f of X as X approaches 3 and just from an inspection you can see that the function is not defined when X is equal to 3 you get 0 over 0 it's not defined so to answer this question let's try to rewrite the same exact function definition slightly Suppose $f''=f$ and consider $g(x)=(f'(x)f(x))e^{x}$ Then $$ g'(x)=(f''(x)f'(x))e^{x}(f'(x)f(x))e^{x}=0 $$ Therefore $g(x)$ is constant Since $$ g(0)=0 $$ we have $f'(x)f(x)=0$, for every $x$ Therefore $f'=f$ Consider $$ h(x)=f(x)e^{x} $$ Then $h'(x)=f'(x)e^xf(x)e^x=0$ so also $h$ is constant Since $h(0)=0$, we are done



Resolutions Graphiques
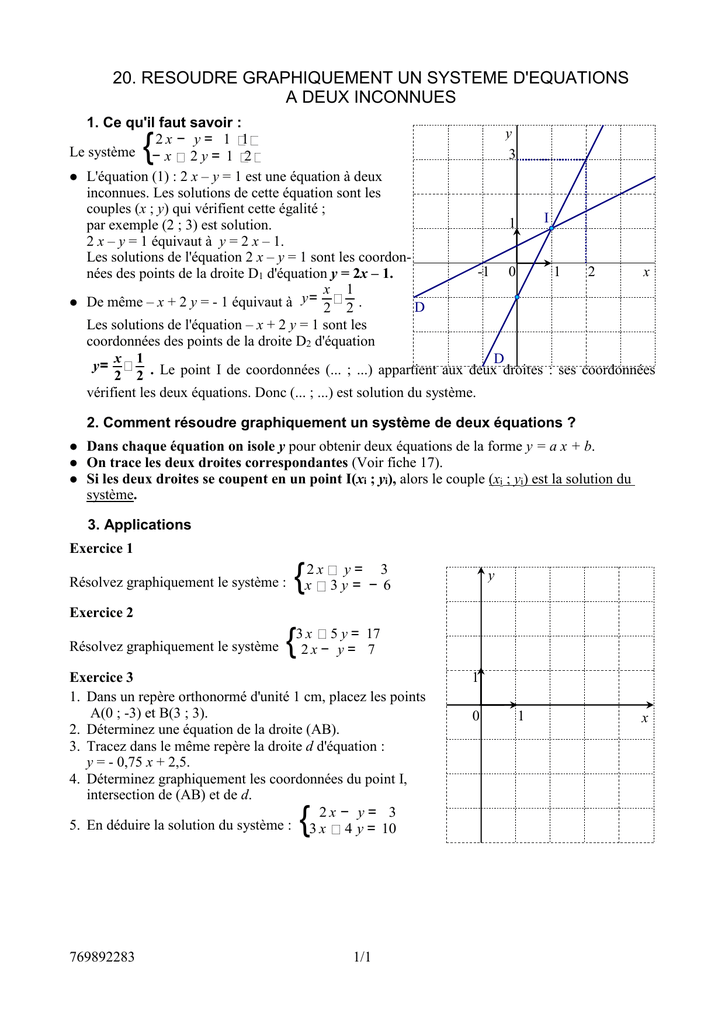



Resoudre F X 0 Graphiquement




Resoudre Graphiquement Une Equation De La Forme F Left X Right K F Left X Right Ge K Ou F Left X Right Le K Generalites Sur Les Fonctions Fiche Exercices Maths 1ere Stl




On Considere Les Fonctions F Et G Representees Graphiquement Dans Le Repere O I J 1 Quel Est Nosdevoirs Fr
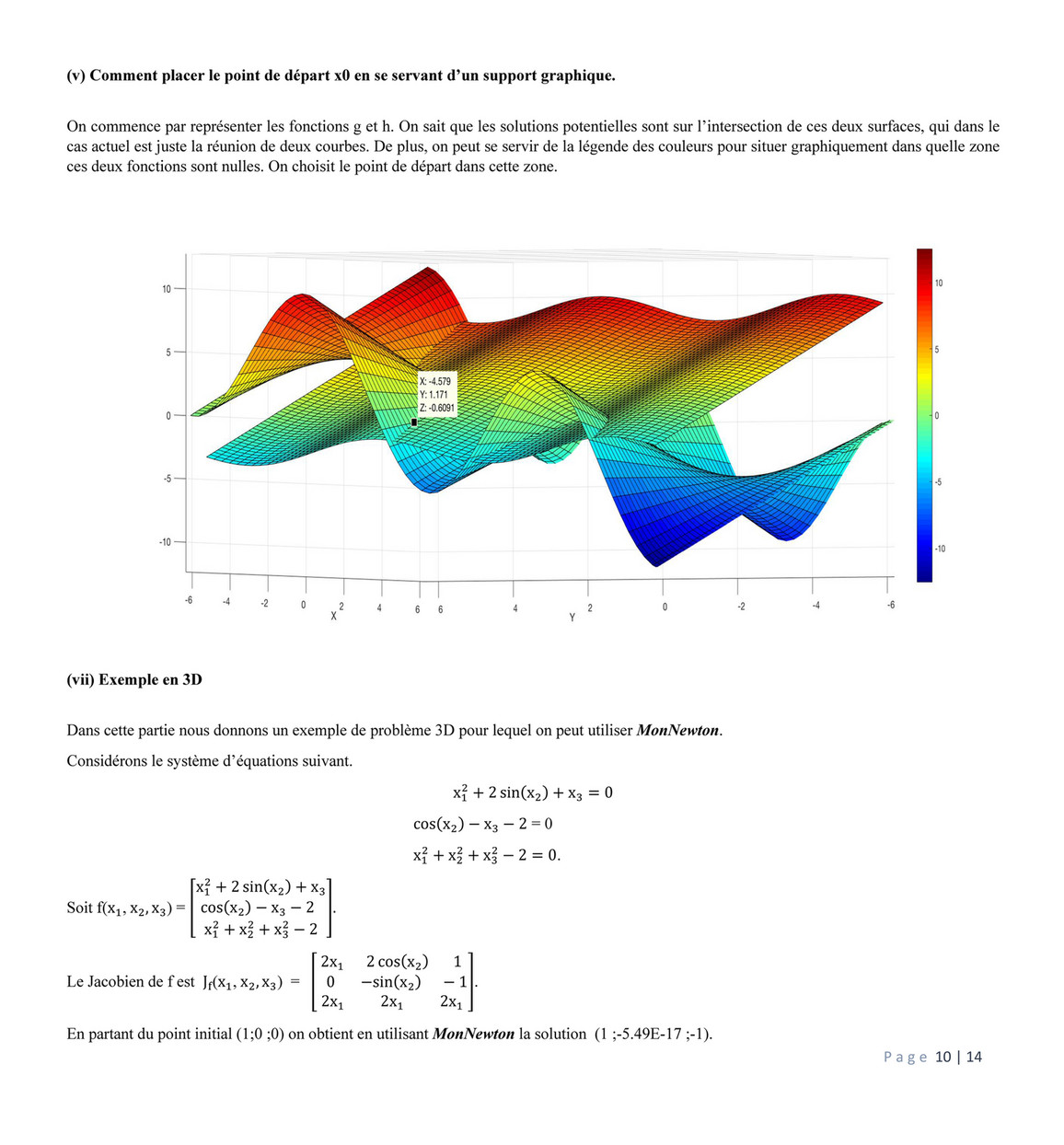



My Publications Numerical Calculation Project 1 Page 1 Created With Publitas Com




Variations Et Courbes Representatives De Fonctions Fiche De Revisions Pour 1re L Etudiant




All About Mathematics Posts Facebook




Resoudre Graphiquement F X G X 2nde Exercice Mathematiques Kartable




Sin X 0




Le Plan Est Muni D Un Repere Orthonorme O I J D Unite 1 Metre Soit F La Fonction Definie Sur 00



Representer Graphiquement Une Suite Un F N Et Un 1 F Un
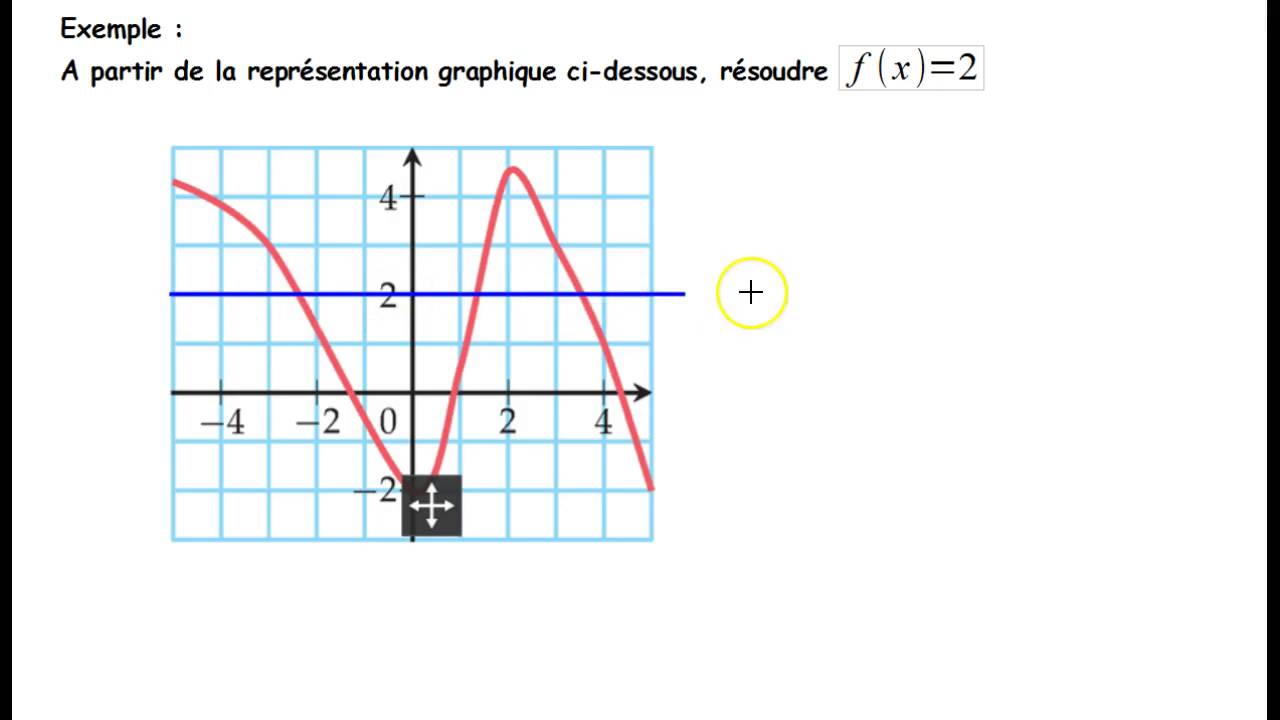



Resoudre Graphiquement F X K Youtube



Ijms Free Full Text How Machine Learning Methods Helped Find Putative Rye Wax Genes Among Gbs Data Html



Test D Activites Mentales N 7 Ppt Telecharger



Calameo Pdf Downloader



Lognormal Freakonometrics



2g Representer Graphiquement Les Fonctions Comment Resoudre F X K Graphiquement Youtube



Cours 3 Resolution Graphique D Inequations Manuel Numerique Max Belin
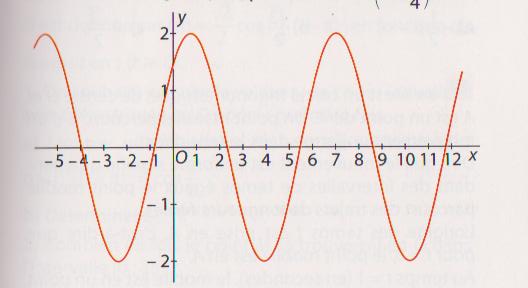



Resoudre Graphiquement L Equation F X 0 Forum De Maths
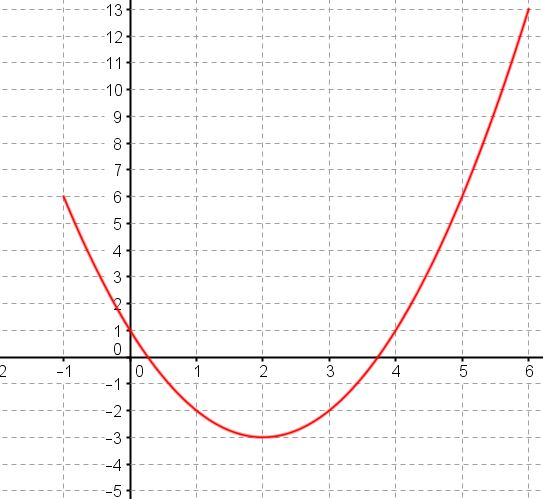



Maths Lycee Fr Exercice Corrige Chapitre Fonctions Generalites




Comment Representer Graphiquement Une Fonction Affine Pdf Cours Exercices Examens



2




Svp C Edt Urgent 1 Determiner Graphiquement Les Solutions Dans 2 4 De L Equation X 2 Nosdevoirs Fr




Epingle Par Marwahammoudi Sur Disney Mathematiques Les Determinants Sciences Experimentales




How To Use Graph To Determine Where F X 0 And F X 0 Mathematics Stack Exchange




Math X Tle S Specifique Complet Calameo Downloader



Exercice 03 Resolutions Graphiques Les Mathematiques Au Lycee Aiguerande




Resoudre Graphiquement Une Inequation Du Type F X K 2nde Exercice Mathematiques Kartable




La Sante June 9 21 Online Event Allevents In
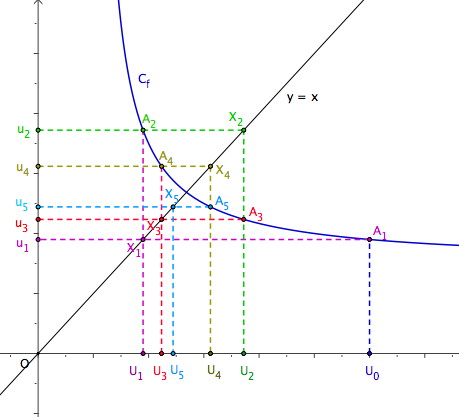



Representer Graphiquement Les Termes D Une Suite Cours Exercices Et Videos Maths



Q Tbn And9gctd9nw2 0u01xazm6kzrgyoi Avw Udvnn7xdvttur5wbcxrttt Usqp Cau




A Mathematical Model Of Tumour Angiogenesis Growth Regression And Regrowth Journal Of The Royal Society Interface



From Circle To Ml Via Batman Part Ii By Jasdeep Grover Towards Data Science




Ex 52 On Considere Deux Fonctions F Et G Definies Par Nosdevoirs Fr




Quelq Un Pourrait M Aider S Il Vous Plait On Considere Une Fonction F Definie Sur 8 3 Dontla Nosdevoirs Fr
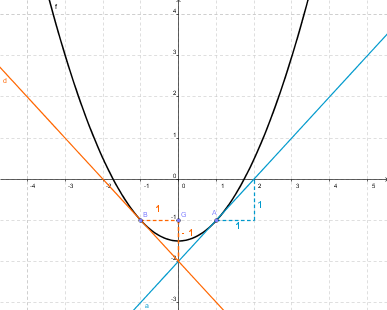



Determiner Graphiquement F X Forum Mathematiques



Resoudre Graphiquement F X Superieur A 0
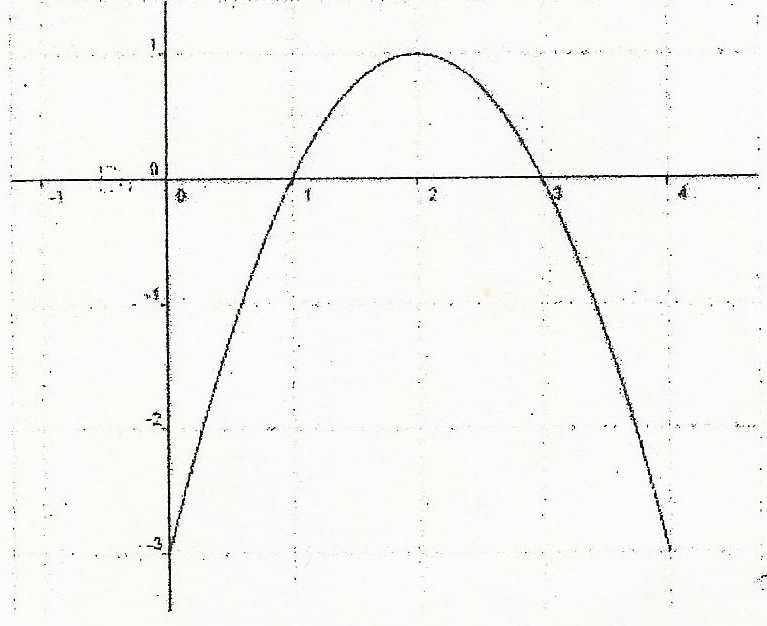



Determiner Graphiquement Les Solutions Forum Mathematiques




Sujet 1 Automatismes Calcul Numerique Et Algebrique Sti2d J Ai En Maths




How To Graph A Quadratic Equation 10 Steps With Pictures




Bonjour Determinez Graphiquement F 0 F 1 F 2 Merci Pour Votre Aide Car Je Ne Sais Pas Du Nosdevoirs Fr
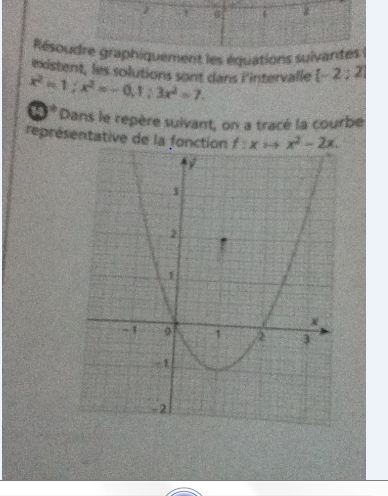



Fonction Forum Mathematiques Seconde Fonctions




Find All Values X A Where The Function Is Discontinuous For Each Point Of Discontinuity Give A F A If It Exists B Lim X A F




Tcs Maths Posts Facebook
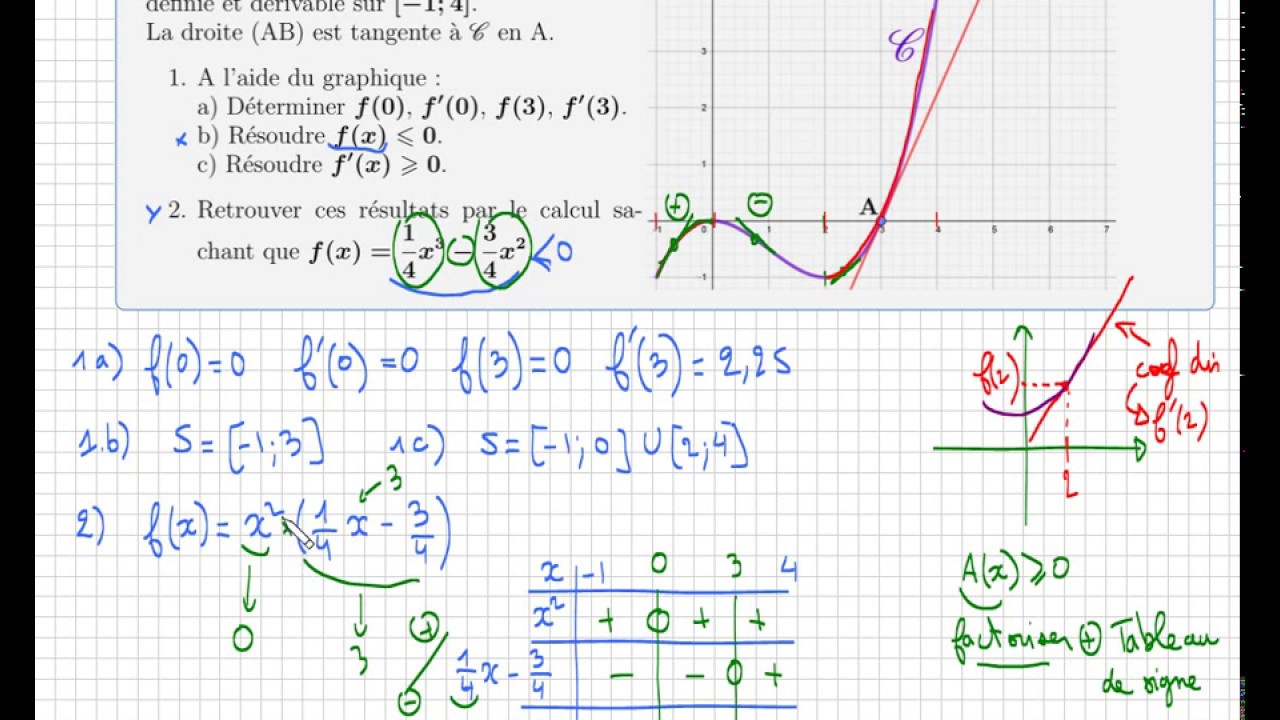



Derivation Resoudre Graphiquement Et Par Le Calcul F X 0 Lire F A Important Youtube




Resolution Graphique D Une Equation De La Forme F X G X Youtube
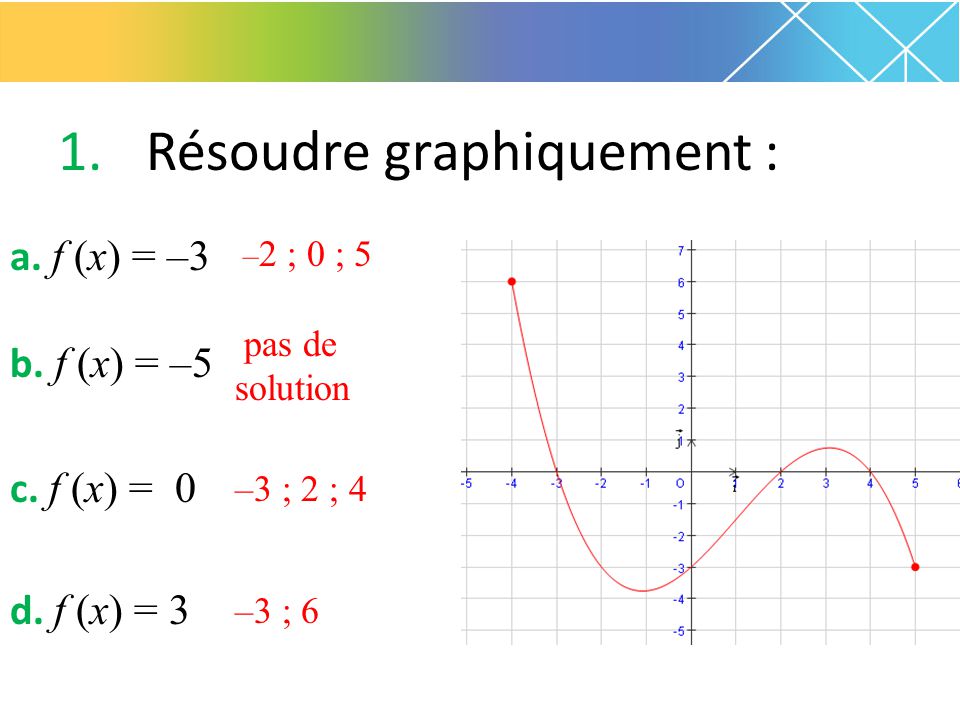



Nombres De Solutions D Une Equation 1 Resoudre Graphiquement A F X 3 B F X 5 C F X 0 D F X Ppt Download



What Does F 0 Represent On The Graph Of F X Quora



2



Representer Graphiquement Une Fonction Lineaire Assistance Scolaire Personnalisee Et Gratuite Asp



Fonction Forum Mathematiques Seconde Fonctions
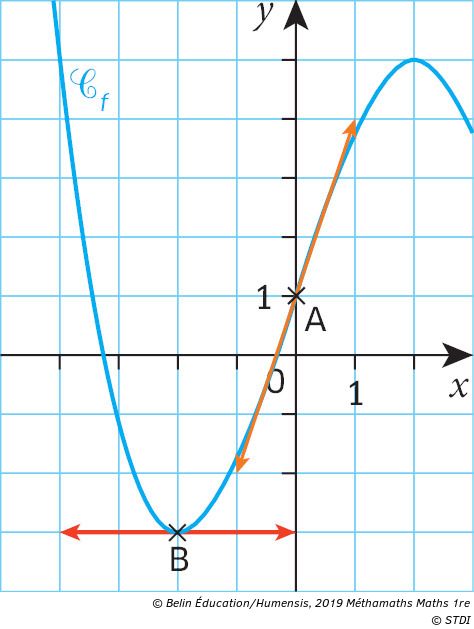



Cours 2 Tangentes A Une Courbe Et Fonction Derivee Manuel Numerique Max Belin




Med Yassine Mzah Math Photos Facebook
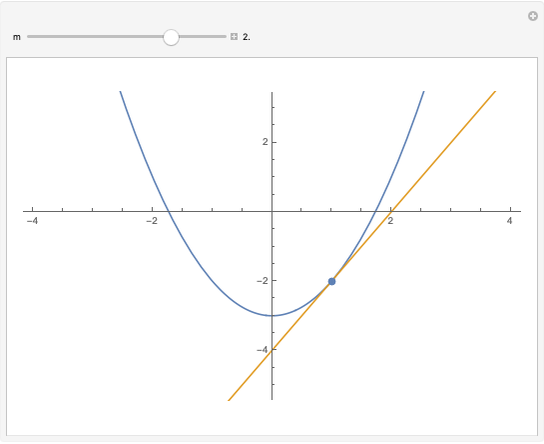



Finding A Tangent Line To A Parabola Wolfram Demonstrations Project




2 Resolution Graphique D Equations Du Type F X K Et F X G X Lelivrescolaire Fr




2 Resolution Graphique D Equations Du Type F X K Et F X G X Lelivrescolaire Fr
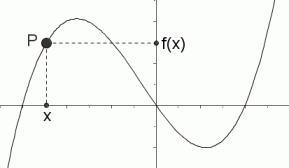



Graphical Interpretation Of Sentences Like F X 0 And F X 0



Arxiv Org Pdf 1912




Determiner Graphiquement La Valeur De F A 1ere Methode Mathematiques Kartable



Resoudre Graphiquement Une Inequation
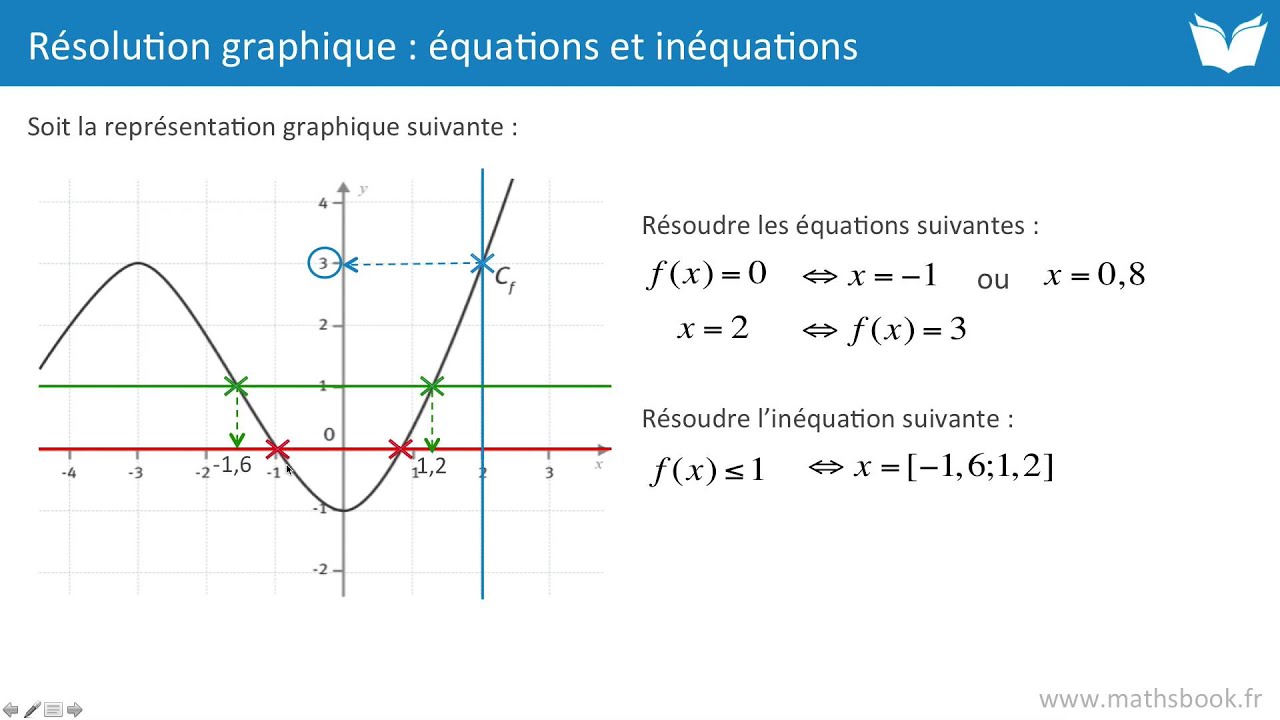



Resolution Graphique D Equations Et D Inequations Cours De Maths Youtube
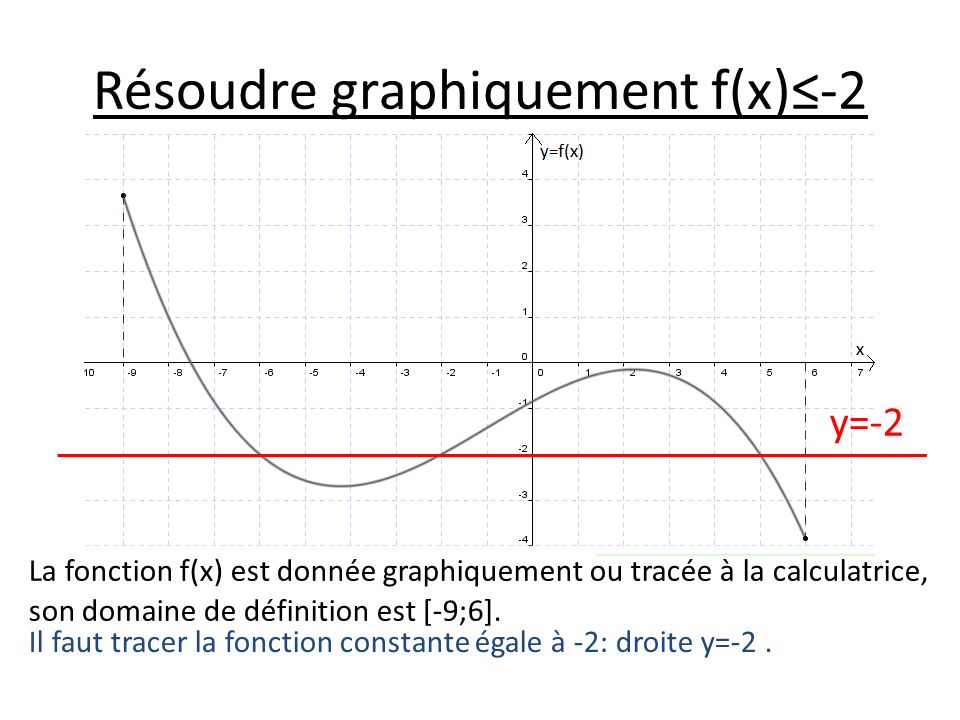



Resoudre Graphiquement F X 2 Ppt Telecharger




2nde Resoudre Graphiquement L Equation F X G X Youtube




Comment Determiner Graphiquement La Valeur D Un Nombre Derive D Une Fonction Youtube
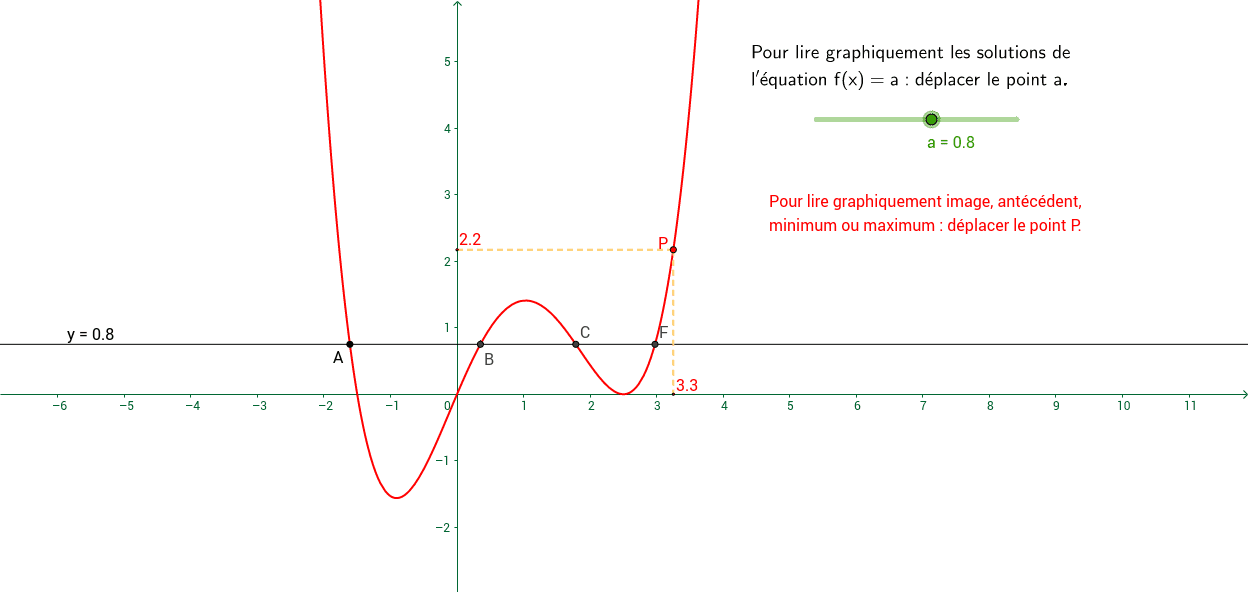



Image Antecedent Extremum Solutions De L Equation F X A Geogebra




Resolutions Graphiques Maxicours
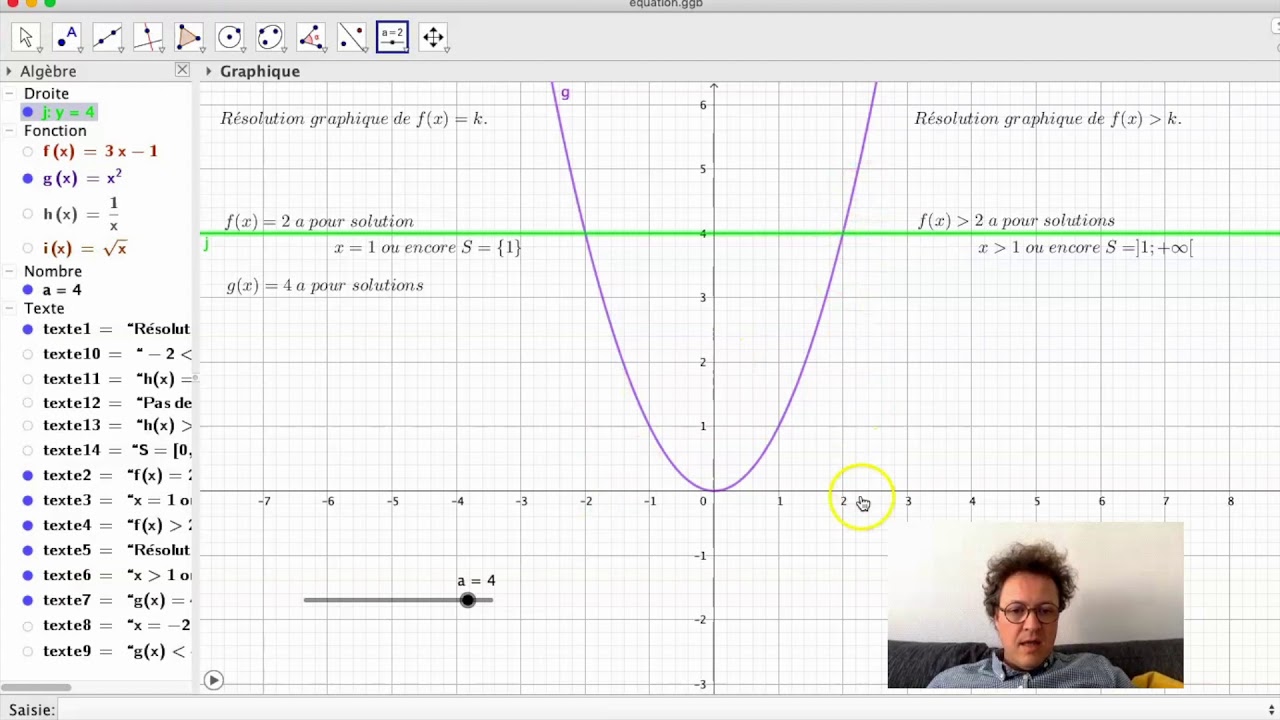



2g Representer Graphiquement Les Fonctions Comment Resoudre F X K Graphiquement Youtube




2nde Comment Resoudre Les Equations Du Type F X K



Resolutions Graphiques De Fonctions En T Es Et T S Conseils Et Astuces Pour Progresser En Maths Et En Physique




Coucou Je Dois Resoudre Graphiquement 1 F X 0 2 F X 3 F X Gt 1 Merci De Me Repondre Si Nosdevoirs Fr




One To One Functions Inverse Function A Function F Is One To One If For Each X In The Domain Of F There Is Exactly One Y In The Range And No Y In The




Resoudre Graphiquement Dans R Les Inequations Suivantes
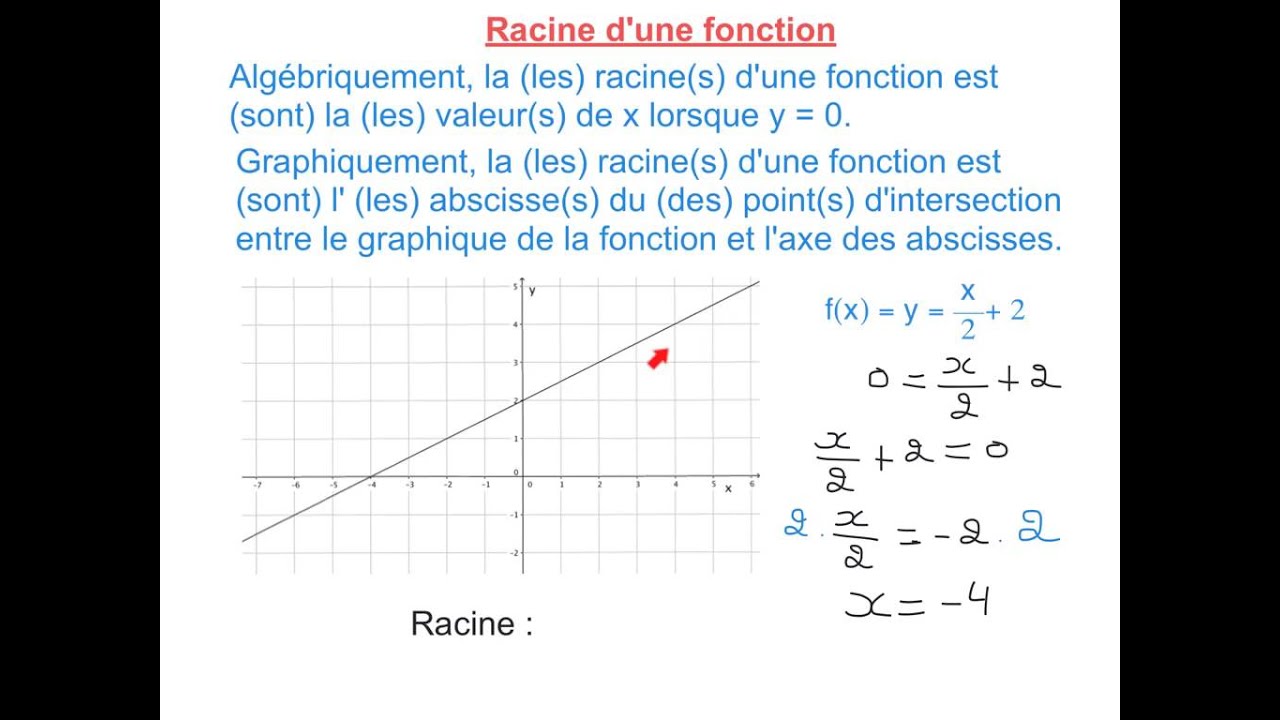



8 4 Racine D Une Fonction Youtube
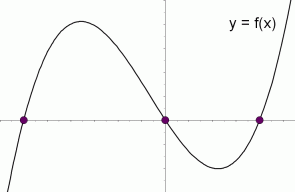



Graphical Interpretation Of Sentences Like F X 0 And F X 0




Resoudre Graphiquement F X G X 2nde Exercice Mathematiques Kartable



0 件のコメント:
コメントを投稿