Calculus Evaluate limit as x approaches infinity of f (x) lim x→∞ f (x) lim x → ∞ f ( x) Evaluate the limit of f (x) f ( x) which is constant as x x approaches ∞ ∞F (x) as x approaches a from theOn the graph of a function f (x), a vertical asymptote occurs at a point P = (x0,y0) if the limit of the function approaches ∞ or −∞ as x → x0 For a How to find limit x approaches 0Answer by richard1234(7193) (Show Source) You can put this solution on YOUR website!
2 2 The Limit Of A Function Calculus Volume 1
Lim x approaches infinity f(x)=0 graph
Lim x approaches infinity f(x)=0 graph-Alternatively, x may approach p from above (right) or below (left), in which case the limits may be written as → = or → = respectively If these limits exist at p and are equal there, then this can be referred to as the limit of f(x) at p If the onesided limits exist at p, but are unequal, then there is no limit at p (ie, the limit at p does not exist)Find the limitlim x = 0 sin(3x)/x



Calculus Limit Function Take The Limit As X Approaches
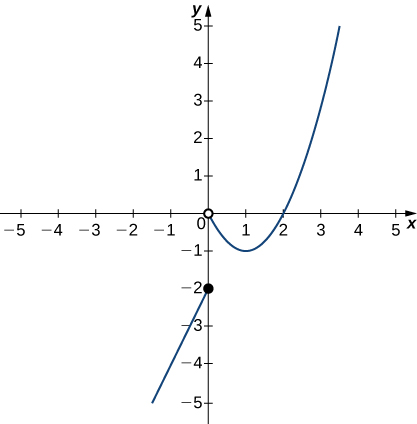
Answer to Sketch the graph of an example of a function that satisfies all of the given conditions limit as x approaches 3 of f(x) = infinity,Lim F X 0 Graph, 11X1 T09 08 implicit differentiation (10), The graph of the functions f(x)and g(x) are given below, Graphing rational functions andStack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their
3/7/21 Lim x approaches infinity f(x)=0 graphSketch the graph of a function f that satisfies the given values f(0) is undefined lim x > 0 f(x) = 4 f(2) = 6 lim x > 2 f(x) = 3 Solution From the given question, We understood that the functions is undefined when x = 0 When the value of x approaches 0 from left hand side and right hand side, limit value will approaches to 4 Question If lim(f(x)/x1/4/18 We say that "the limit of `5/x` as x approaches infinity is `0`" We write this in mathematical notation as `lim_(x>oo)(5/x)=0` Here is the graph of `y=5/x` (for positive `x`), showing the `y`value gets closer to `0` as `x` increases 10 30 40 50 60 70 80 05 1 15 2 25 3 x y Open image in a new pageHere we say that lim x→0 g(x) = 1 Note that g(0) is undefined Graphical Approach to Limits Example 3 The graph below shows that as x approaches 1 from the left, y = f(x) approaches 2 and this can be written as lim x→1f(x) = 2 As x approaches 1 from the right, y = f(x) approaches 4 and this can be written as lim x→1 f(x) = 4 Note that the left and right hand limits and f(1) = 3
Evaluate the limits at infinity Since f is a rational function, divide the numerator and denominator by the highest power in the denominator x 2 We obtain lim x → ± ∞ x 2 1 − x 2 = lim x → ± ∞ 1 1 x 2 − 1 = − 1 Therefore, f has a horizontal asymptote of y = − 1 as x → ∞ and x → − ∞ Step 417/1/ We need to know the behavior of \(f\) as \(x→±∞\) In this section, we define limits at infinity and show how these limits affect the graph of a functionLimits to Infinity Calculator Get detailed solutions to your math problems with our Limits to Infinity stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!



Calculus I Infinite Limits



Q Tbn And9gcsazoostrpnrtf4rizmcmms5l1qte8refyfv4dl3jsntkt60xol Usqp Cau
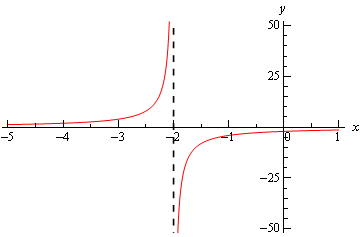
A function cannot cross a vertical asymptote because the graph must approach infinity In Example 425, we show that the limits at infinity of a rational function f (x) = p (x) q (x) lim x → ∞ 2 e x = 0 = lim xLim x → ∞ f(x) = 0 lim x → ∞ f(x) = 0 An example with a function that has a limit of two at infinity For the function in the graph below, we first consider the behavior of f(x) as as x increases without bound, or in other words, we consider what happens to f(x) as we move farther and farther to the right on the graphLim (x^2 2x 3)/(x^2 2x 3) as x > 3;



Calculus How Is The Answer To Lim X Pi 2 Tan X Negative Infinity And Positive Infinity Quora




2 6 Limits At Infinity X X As X Approaches Infinity F X As X Gets Larger And Larger F X As X Gets Larger And Larger In The Negative Direction Ppt Download
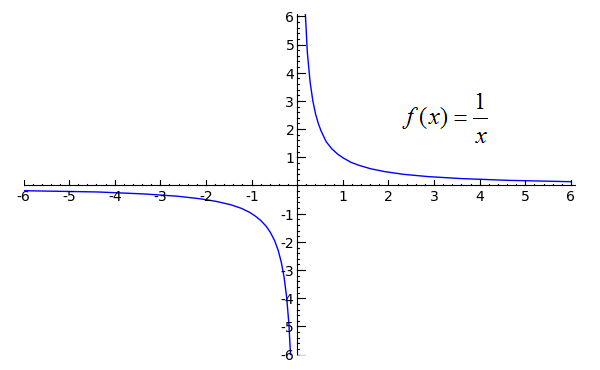
Free Limit at Infinity calculator solve limits at infinity stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyThe limit of 1 x as x approaches Infinity is 0 And write it like this lim x→∞ ( 1 x) = 0 In other words As x approaches infinity, then 1 x approaches 0 When you see "limit", think "approaching" It is a mathematical way of saying "we are not talking about when x=∞, but we know as x gets bigger, the answer gets closer and closer to 0"Evaluate limit as x approaches infinity of (3x2)/ (2x1) lim x→∞ 3x − 2 2x 1 lim x → ∞ 3 x 2 2 x 1 Take the limit of each term Tap for more steps Divide the numerator and denominator by the highest power of x x in the denominator, which is x x lim x → ∞ 3 x x − 2 x 2 x x 1 x lim x → ∞ 3 x x 2 xCalculus Evaluate limit as x approaches infinity of f (x) lim x→∞ f (x



1 4 Limits At Infinity And Horizontal Asymptotes End Behavior Mathematics Libretexts




Lecture 6 Limits With Infinity
If lim f(x) = L1 as x approaches a from the left and lim f(x) = L2 as x approaches a from the right lim f(x) as x approaches a exists only if L1 = L2 Answer True This is an important property of the limits Question 9 True or False lim sin x as x approaches very large values (infinity) is 1 or 1Evaluate lim xS0 S f 1x2, lim x 0S f 1 x2, and lim x 0 f 1 x2 T b Create a graph that gives a more complete representation of f 4 2 0 2 4 x 15 10 5 y 00 50 100 x 2 y Technology Exercises 49–56 Asymptotes Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions 49 fLimit as x approaching 0 of xln (x) \square!




Given The Function F X 6x 3 2x 2 The Chegg Com




Find Limit Of X 2 E X As X Approaches Infinity Mathematics Stack Exchange
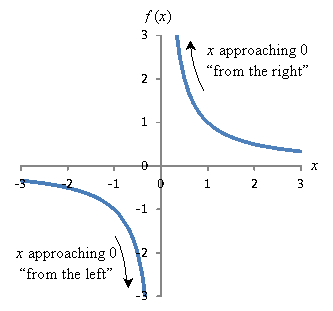
We then say that the values of f (x) become infinite, or tend to infinity We say that as x approaches 0, the limit of f (x) is infinity Now a limit is a number—a boundary So when we say that the limit is infinity, we mean that there is no number that we can name It is important to note that by saying lim x → c f(x) = ∞ we are implicitly stating that \textit {the} limit of f(x), as x approaches c, does not exist A limit only exists when f(x) approaches an actual numeric value We use the concept of limits that approach infinity because it is helpful and descriptive Explanation lim x→∞ (xe1 x −x) = lim x→∞ x(e1 x − 1) = lim x→∞ e1 x − 1 1 x Direct substitution here produces a 0 0 indeterminate form Apply L'Hopital's rule = lim x→∞ d dx(e1 x − 1) d dx 1 x = lim x→∞ e1 x( − 1 x2) − 1 x2 = lim x→∞ e1 x = e 1 ∞



Sage Calculus Tutorial One Sided Limits
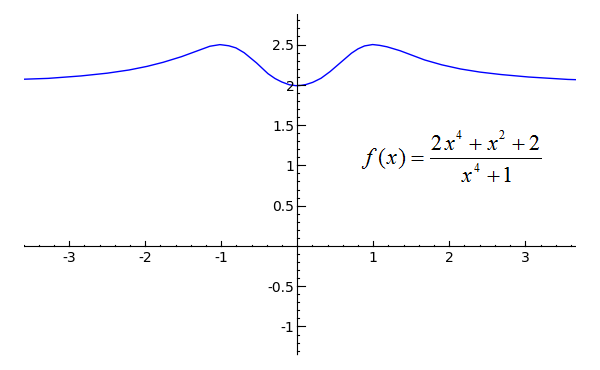



Sage Calculus Tutorial Limits At Infinity
No graph provided After all, the limit as x goes to infinity of this graph(e x − e−x) = − sinh x If f(−x) = −f(x) we say that f(x) is an odd function;Limx → ∞ ( 2x3 − 2x2 x − 3 x3 2x2 − x




How To Find Limits Using Asymptotes Video Lesson Transcript Study Com



What Is The Limit Of 1 X As X Approaches 0 Quora
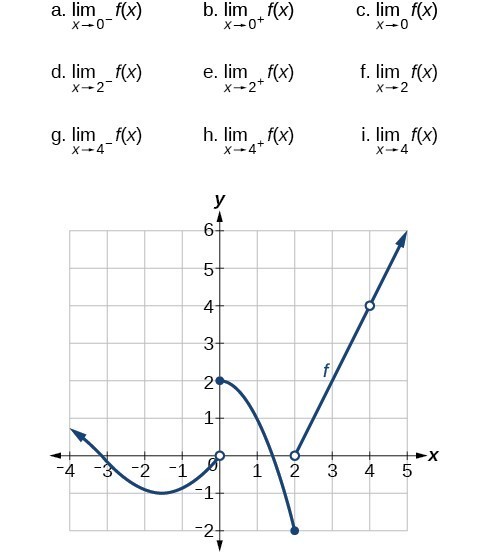
Solution for Sketch a graph of a function f(x) that has the following properties lim as x approaches infinity is f(x)= infinity lim as x approaches 6 fromLim x→0 (3x 1) = 1It#appearsthat,#asx#getscloser#and#closer#to#2#from# theleft,f(x)#getscloser#and#closer#to#05# Wesaythat*thelimit*of*f(x),*as*x*approaches*2*from*the left,*equals*05* * € x→2− limf(x)=05% Thisvalueisalsocalled"theleftFhand*limitas%x% approaches2"% It#also#appearsthat,#asx#getscloser#and#closer#to#2# from#the#right,#f(x)#getscloser#and#closer#to#0




1 6 Limits Involving Infinity Infinite Limits Definition The Notation Read As The Limit Of Of F X As X Approaches A Is Infinity Means That The Ppt Download
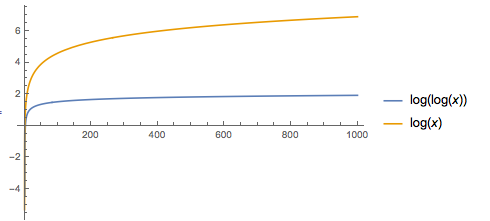



How Do You Find The Limit Of Ln X 1 X As X Approaches Infinity Socratic
In proving a limit goes to infinity when x x x approaches x 0 x_0 x 0 , the ε \varepsilon εδ \delta δ definition is not needed Rather, we need only show that the function becomes arbitrarily large at values close to x 0 x_0 x 0 Prove lim x → ∞ 1 x 2 = 0 \lim_{x \rightarrow \infty} \frac{1}{x^2} = 0 x → ∞ lim x 2 1 = 0N=1 are also points on the graph of the function f(x) = 1/x for x > 0 As x gets larger, f(x) gets closer and closer to zero In fact, f(x) will get closer to zero than any distance we choose, and will stay closer We say that f(x) has limit zero as x tends to infinity, and we write f(x) → 0 as x → ∞, or lim x→∞ f(x) = 0 5 10 x 0Suppose f(x) = x^(lnx) a Verify that lim as x approaches 0 f(x)=0 and lim as x app infinity f(x)=0 Graph f on the interval 0,10 b A remarkable result of third semester calculus is that the integral from inf to inf of e^(x^2)dx= sqrt (pi) Assume that his result is correct, and use it to show that the integral from 0 to inf




Limits



Solving Limits At Infinity Intuition And Examples
The line x=c is a veritcal asymptote of the graph of the function f Which of the following statements cannot be true?Question If lim(f(x)/x)=5 as x approaches 0, then lim(x^2(f(1/x^2))) as x approaches infinity is equal to (a) 5 (b) 5 (c) infinity (d) 1/5 (e) none of these The answer key says (a) 5 So this is what I know Since MathLimit (1 1/n)^n as n > infinity;
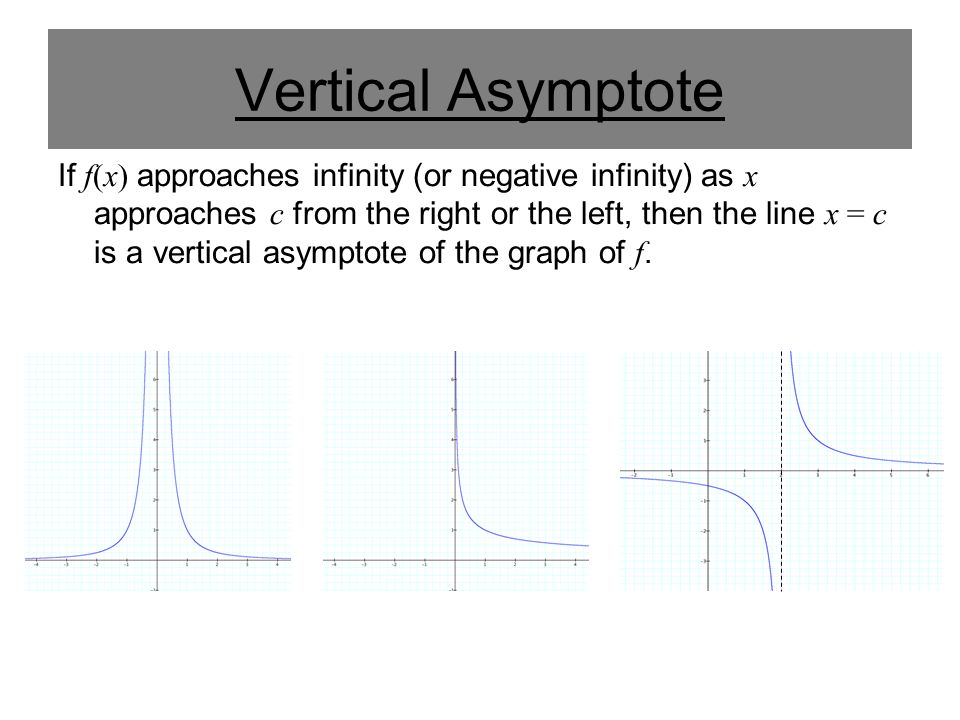



Section 1 5 Infinite Limits Ppt Download




2 2 The Limit Of A Function Calculus Volume 1
Lim f(x) = Infiiite X > Infinite How do you graph this Question Answered stepbystep Lim f(x) Comments (0) Answer & Explanation Solved by verified expert The graph is shown in the explnation section Stepbystep explanation Consider the limitGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Lim ((x h)^5 x^5)/h as h > 0;




Limit As X Approaches Infinity For Log Of Greatest Integer Over X Youtube



Calculus Limits
4/7/21 √70以上 lim f(x) x approaches 0 graph How to find limit x approaches 0 Get link;Answer to Using statements, prove that lim(x approaches infinity) of 1/x equals 0 By signing up, you'll get thousands of stepbystep solutions25/4/ Graph Would the following statement be true for the graph above As x approaches infinity, f(x) approaches 0 How would I write this in mathematical terms?




How Can E X Seemingly Approach 0 As X Approaches Negative Infinity Mathematics Stack Exchange




Limits At Infinity Infinite Limits And Asymptotes
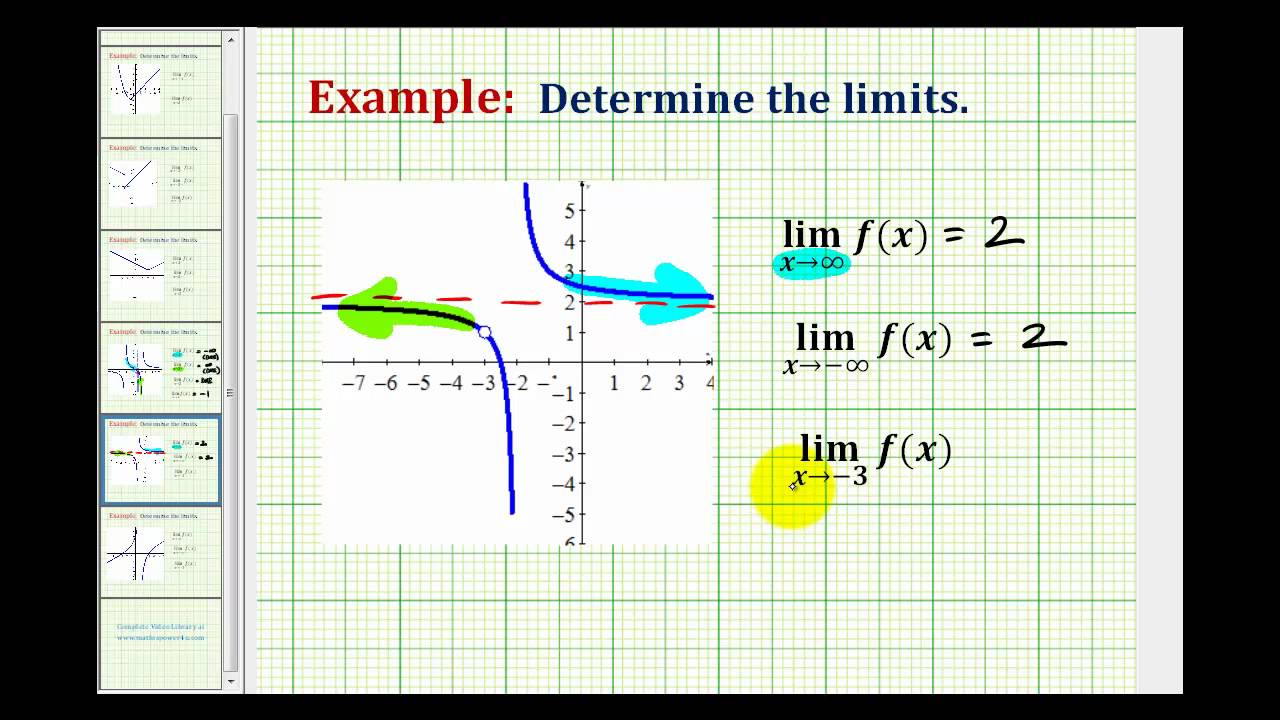
Limits at infinity of quotients (Part 1) Limits at infinity of quotients (Part 2) Practice Limits at infinity of quotients Limits at infinity of quotients with square roots (odd power) Limits at infinity of quotients with square roots (even power) Practice Limits at infinity of quotients with square roots Next lessonSimilarly, lim x → − ∞ f (x) = L means the function approaches L as x grows infinitely large in the negative direction Estimating Limits at Infinity with Graphs and Tables Example 1 Use the graph below to estimate lim x → ∞ f (x)Here, we would say that the limit of f (x) as x approaches zero from the left is negative infinity and that the limit of f (x) as x approaches zero from the right is infinity The limit of f (x) as x approaches zero is undefined, since both sides approach different values
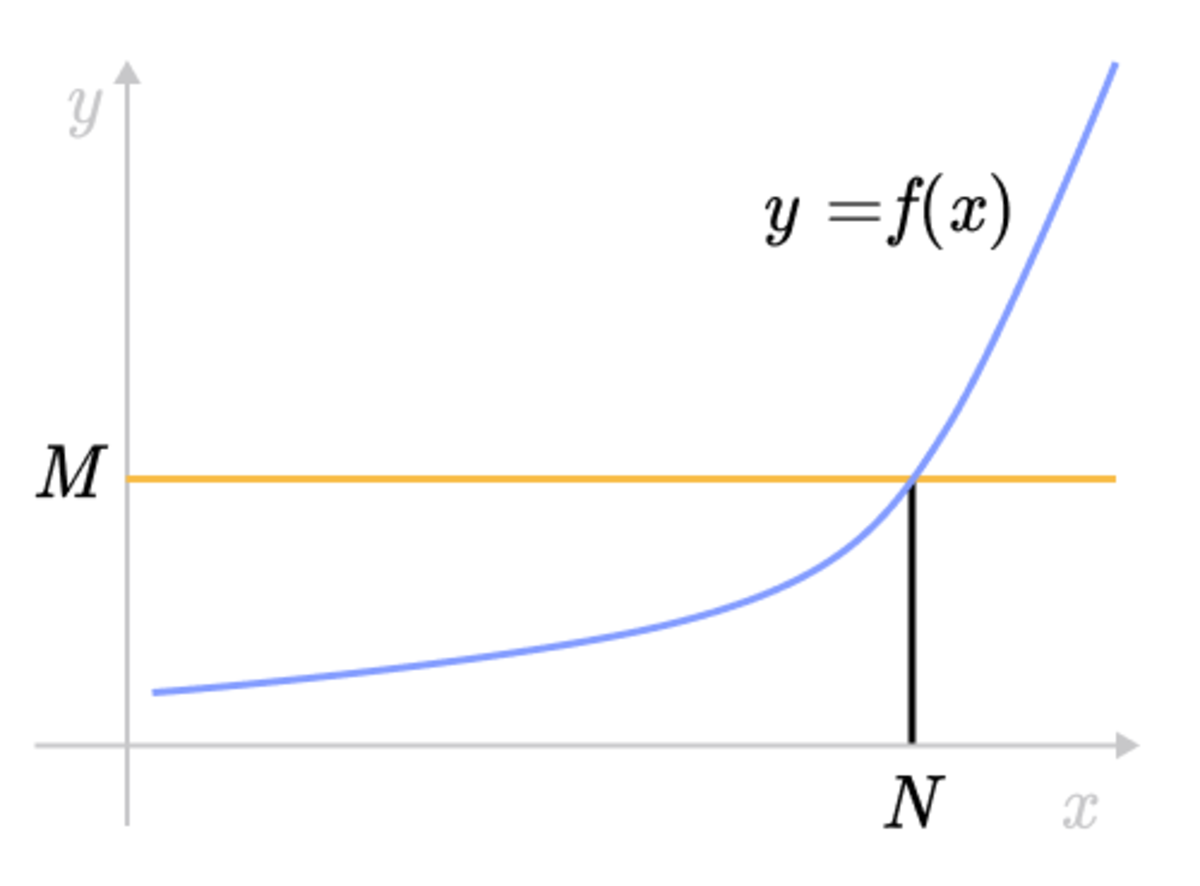



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki



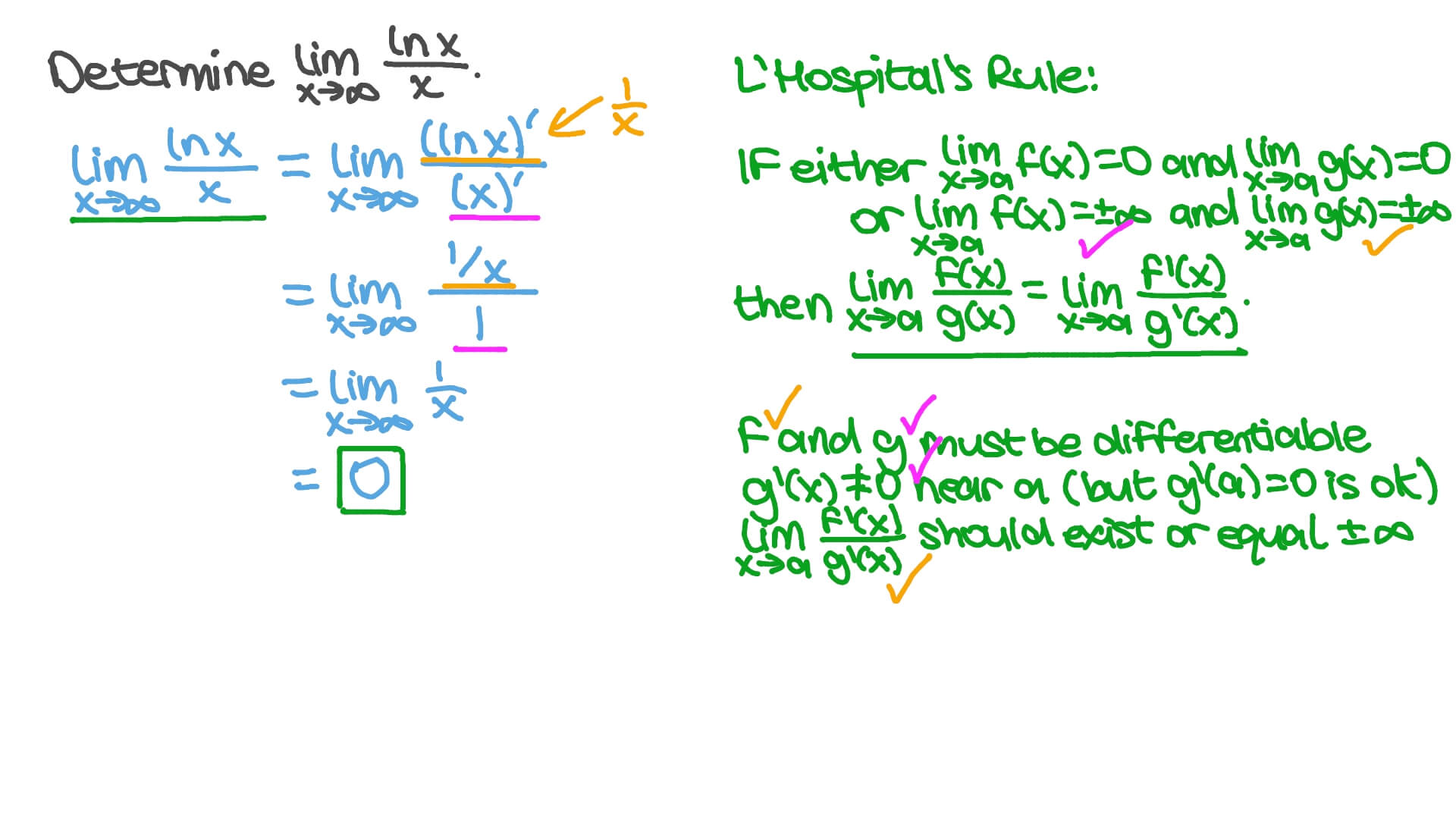
L Hopital S Rule Wikipedia
24/7/15 lim x→0− 1 x = − ∞ this means that the value of your function as you approach zero becomes enormous but negative (try using x = −001 or x = − ) 2 f (x) = 3x 1 as you approach zero from the right or left your function tends to 1!Definition 319 Limit at Infinity In general, we write lim x→∞f(x)= L lim x → ∞ f ( x) = L if f(x) f ( x) can be made arbitrarily close to L L by taking x x large enough If this limits exists, we say that the function f f has the limit L L as x x increases without bound Similarly, we writeSuppose f is a realvalued function and c is a real numberIntuitively speaking, the expression → = means that f(x) can be made to be as close to L as desired, by making x sufficiently close to c In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L" AugustinLouis Cauchy in 11, followed by Karl Weierstrass, formalized the definition of the



Formal Definition Of The Limit



1
Question 4471 What graph indicates lim x > infinity f(x)=3 ? I know tanhx as x approaches infinity is one but 1∞ isn't the correct answer So what I did was I took the limx → ∞lny = limx → ∞xlmtanhx I know that the tanhx = (ex − 1) / (ex 1) but plugging that in, I get lim x → ∞(xln(∞ / ∞)) I am not sure what I am supposed to do there or if I even did it right We're not allowed toThe graph of y = sinh x is symmetric about the origin Recall −that 1sinh xx = (e −e x) As x approaches positive infinity, the value 2 of xe approaches positive −infinity and the value of e x approaches zero lim sinh x = ∞ x




2 6 Limits Involving Infinity Asymptotes Ppt Download




Limits Involving Infinity Section 1 4 Infinite Limits A Limit In Which F X Increases Or Decreases Without Bound As X Approaches C Is Called An Infinite Ppt Download
A Lim as x approaches c from the left f(x)= infinity B lim as x apporaches infinity f(x)=c C f(c) is Please check my Caclulus 1 Find all intervals on which the graph of y=(x^21)/x^2 is concave upward ALim as x approaches infinity (13,x)^(5x) Getting Image Please Wait or Question Lim as x approaches infinity (13/x)^(5x) Related Answer More Related Question & Answers Show that underset(x to 0)(lim) (5^(x) 4^(x) 2^(x) 1)/(5x) is equal toSketch the graph of a function f that satisfies the given values f(0) is undefined lim x > 0 f(x) = 4 f(2) = 6 lim x > 2 f(x) = 3 Solution From the given question, We understood that the functions is undefined when x = 0 When the value of x approaches 0 from left hand side and right hand side, limit value will approaches to 4



Finding Limits Numerical And Graphical Approaches Precalculus Ii



Precalculus How To Calculate Limits For Various Functions Universalclass
For specifying a limit argument x and point of approach a, type "x > a" For a directional limit, use either the or – sign, or plain English, such as "left," "above," "right" or "below" limit sin(x)/x as x > 0;



Limit Of Function Continuous Function Limit At Infinity



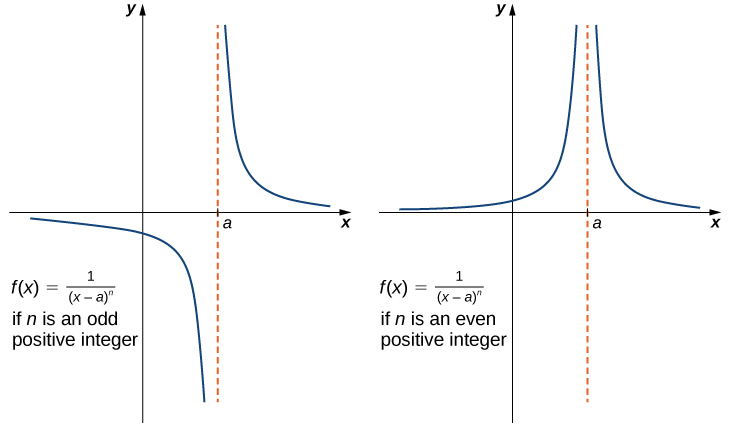
Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora




What S The Limit When X Approaches 1 Socratic



2 2 The Limit Of A Function Calculus Volume 1




Please Show A Step By Step Solution For The Limit As Chegg Com




Connecting Limits At Infinity Notation And Graph Video Khan Academy



Q Tbn And9gcsazoostrpnrtf4rizmcmms5l1qte8refyfv4dl3jsntkt60xol Usqp Cau



Sage Calculus Tutorial Limits At Infinity




Limits At Infinity Infinite Limits And Asymptotes
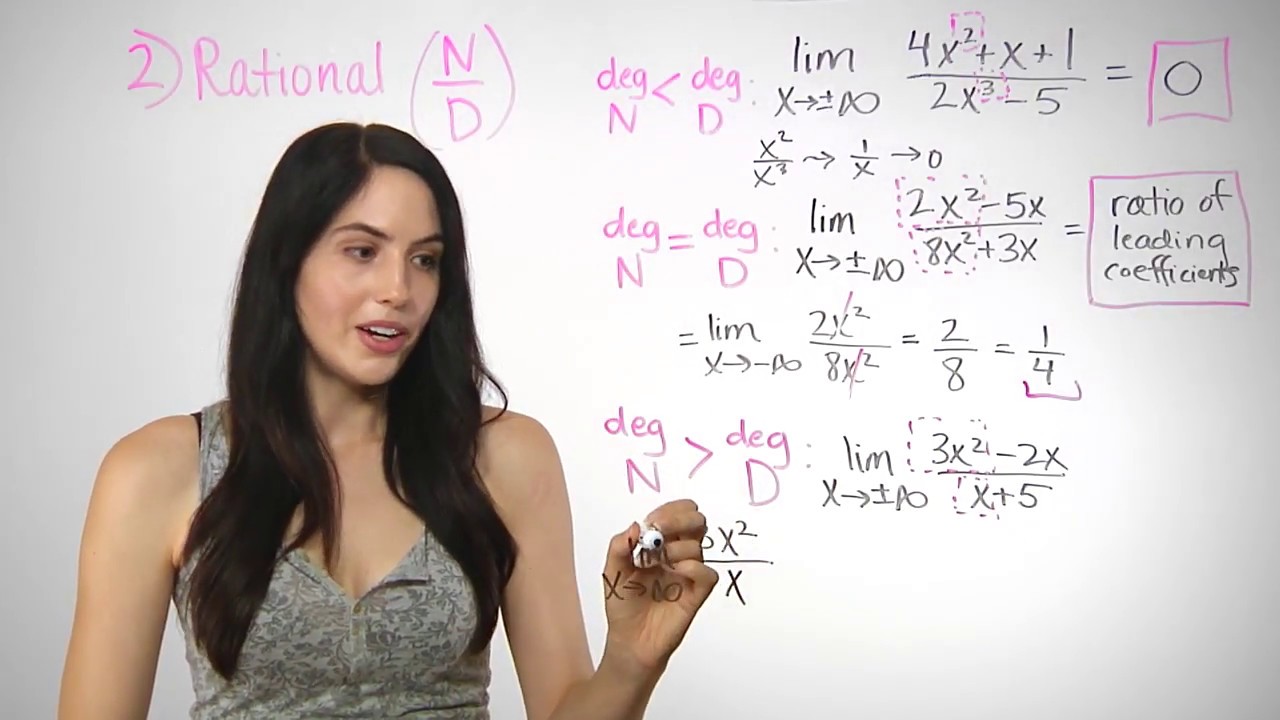



How To Find The Limit At Infinity Nancypi Youtube



Calculus Limit Function Take The Limit As X Approaches




Limits



Question Video Finding The Limit Of Trigonometric Functions Nagwa



Examples Determining Limits At Infinity Graphically Youtube




Introduction To Limits At Infinity Video Khan Academy




Limits




Finding The Limit Free Math Help




End Behavior Of Functions Ck 12 Foundation




Calculus How To Find Limits With Infinity Using The Graph Youtube
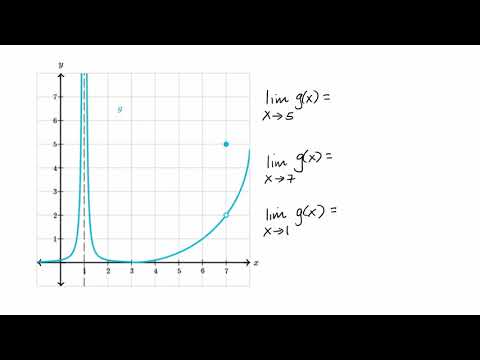



Estimating Limit Values From Graphs Video Khan Academy
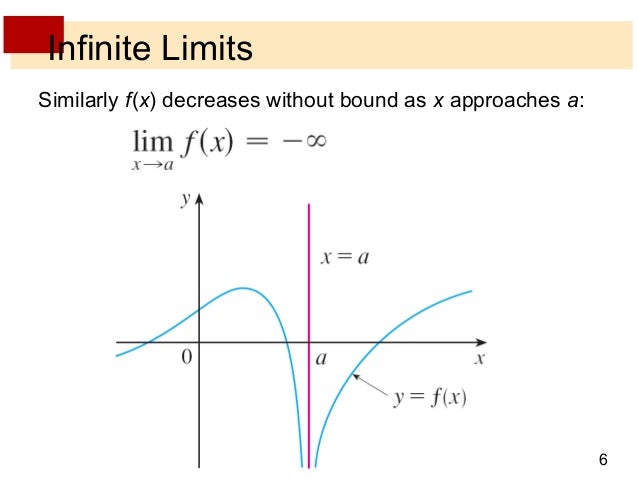



Lecture 6 Limits With Infinity



Does Limit X 0 1 X Exist Quora




Limits Of Transendental Function E 1 X 1 E 1 X 1 As X Approaches Zero Test 1 Youtube
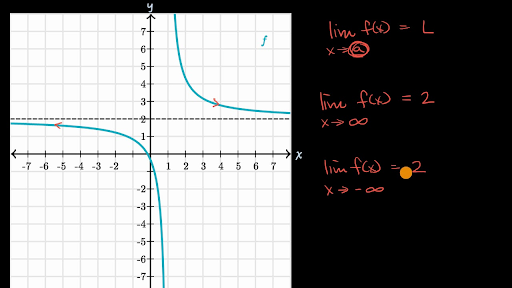



Introduction To Limits At Infinity Video Khan Academy



Finding Limits Graphically




Question Video Finding The Limit Of A Composition Of Rational Functions At Infinity Nagwa



15 11 Limits At Infinity Graphing Calculator By Mathlab User Manual



1 Limits And Differentiation




Limits




Use The Information To Sketch A Graph Of F X A Limit As X Approaches Infinity Of F X 1 B Limit As X Approaches 2 Of F X Infinity C Limit As




Limits
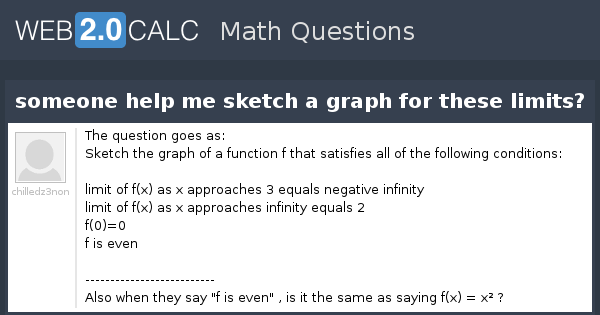



View Question Someone Help Me Sketch A Graph For These Limits
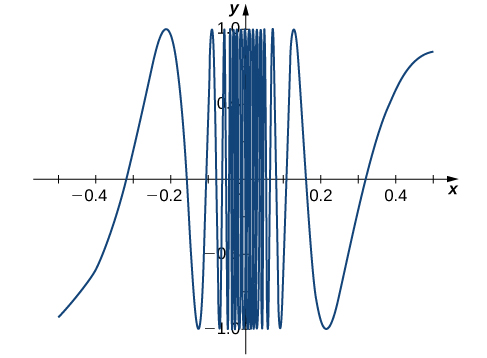



2 2 The Limit Of A Function Calculus Volume 1
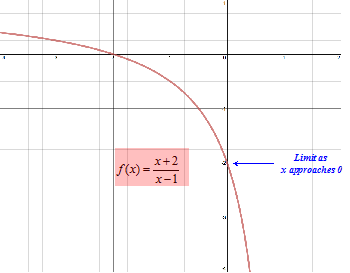



Limits Introduction And One Sided Limits



Calculus Limit Function Take The Limit As X Approaches



Http Www Utm Utoronto Ca Asc Sites Files Asc Public Shared Pdf Tip Sheets Math Rgasc Cmath Limits as x approaches infinity 1117 Pdf
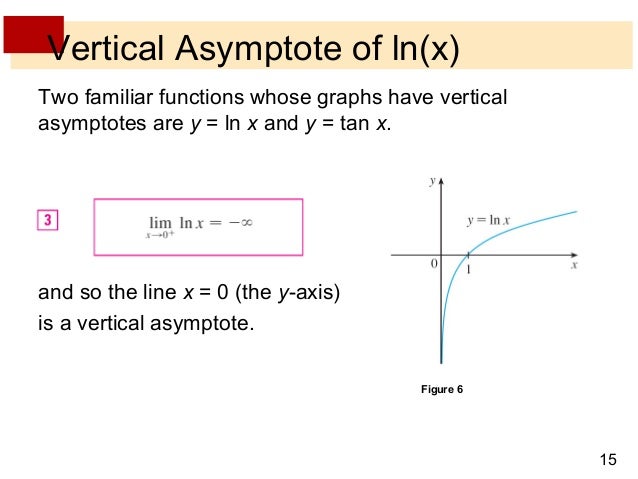



Lecture 6 Limits With Infinity
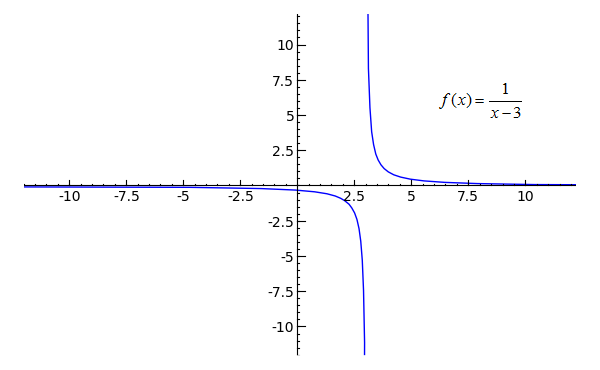



Sage Calculus Tutorial Limits At Infinity
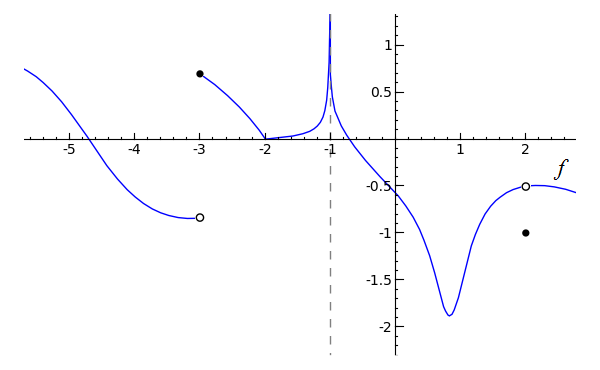



Sage Calculus Tutorial One Sided Limits



Week 3 Limits Involving Infinity And Continuity Ap Calculus




Limits Involving Infinity Section 1 4 Infinite Limits A Limit In Which F X Increases Or Decreases Without Bound As X Approaches C Is Called An Infinite Ppt Download
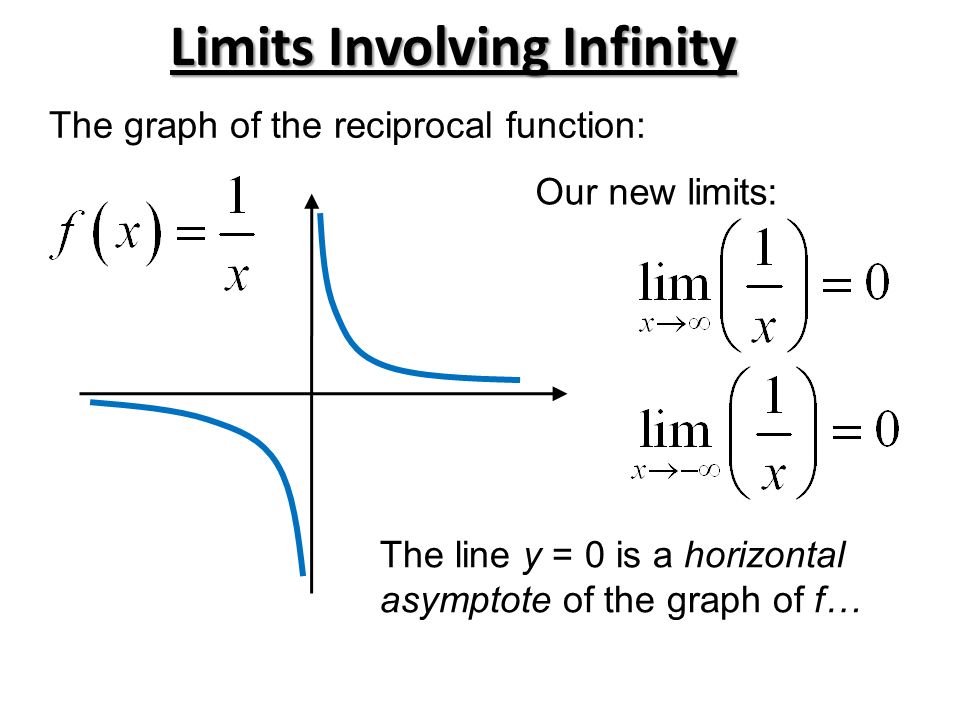



Section 2 2a Limits Involving Infinity We Can Say The Limit Of F As X Approaches Infinity Meaning The Limit Of F As X Moves Increasingly Far To The Ppt Download
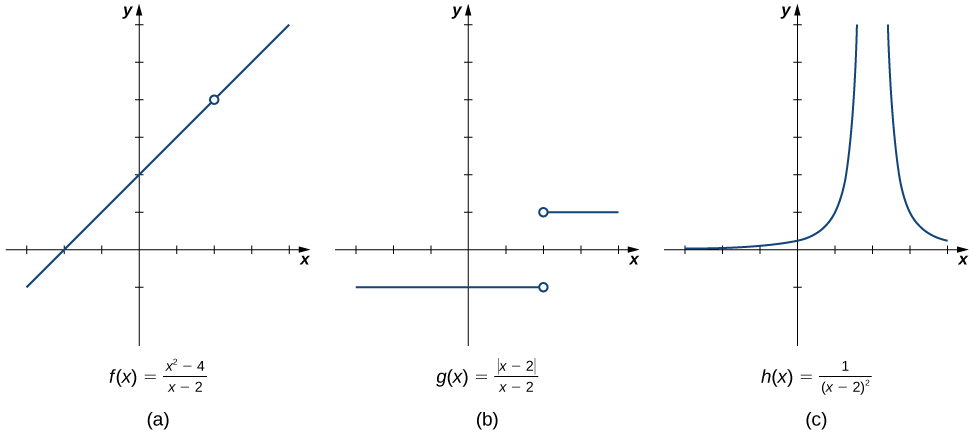



2 2 The Limit Of A Function Calculus Volume 1
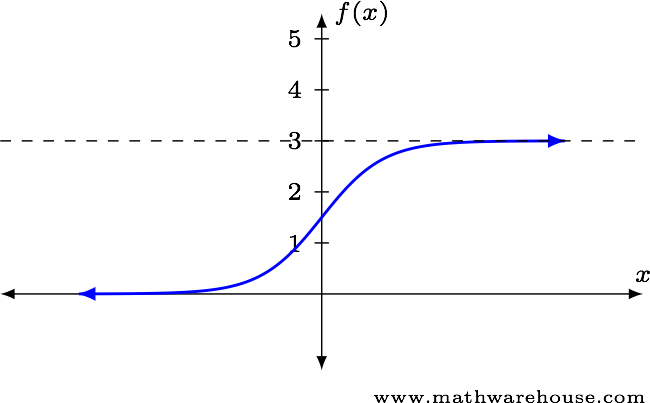



Limits At Infinity Concept How To Solve With Examples




Limits At Infinity Infinite Limits And Asymptotes




7 Determine The Domain Of F X 1x And Graph The Chegg Com




Question 37 For The Function F X Use A Graphing Chegg Com



Calculus Limits




The Squeeze Theorem
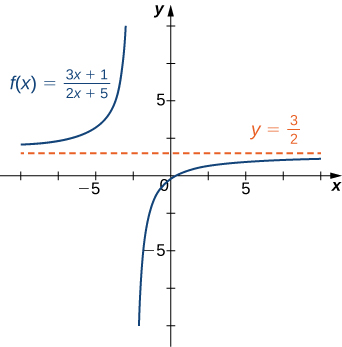



2 5 Limits At Infinity Mathematics Libretexts



Infinite Limits And Vertical Asymptotes Calculus Socratic
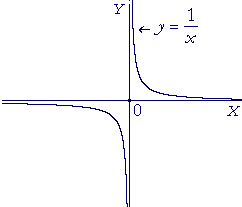



The Limit Infinity An Approach To Calculus




Limits At Infinity Of Quotients Part 1 Video Khan Academy
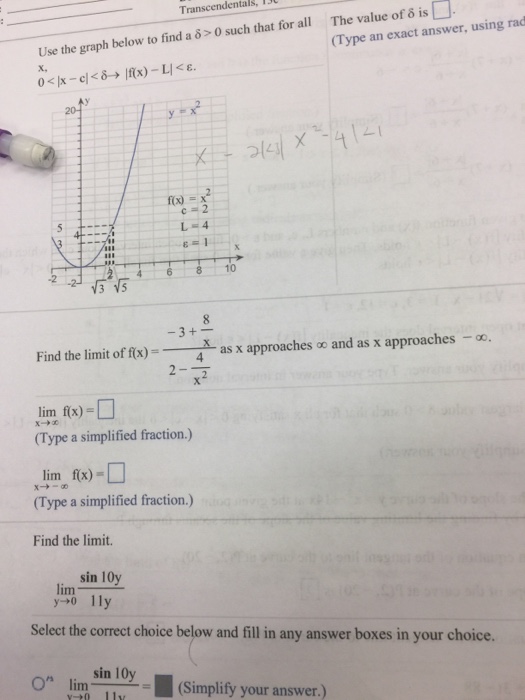



Find The Limit Of F X 3 8 X 2 4 X 2 As X Chegg Com



Solving Limits At Infinity Intuition And Examples




Limits
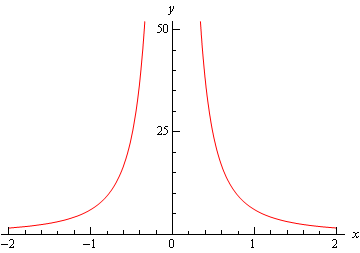



Calculus I Infinite Limits




How To Determine If A Limit Does Not Exist Video Lesson Transcript Study Com



Limit Of Function Continuous Function Limit At Infinity
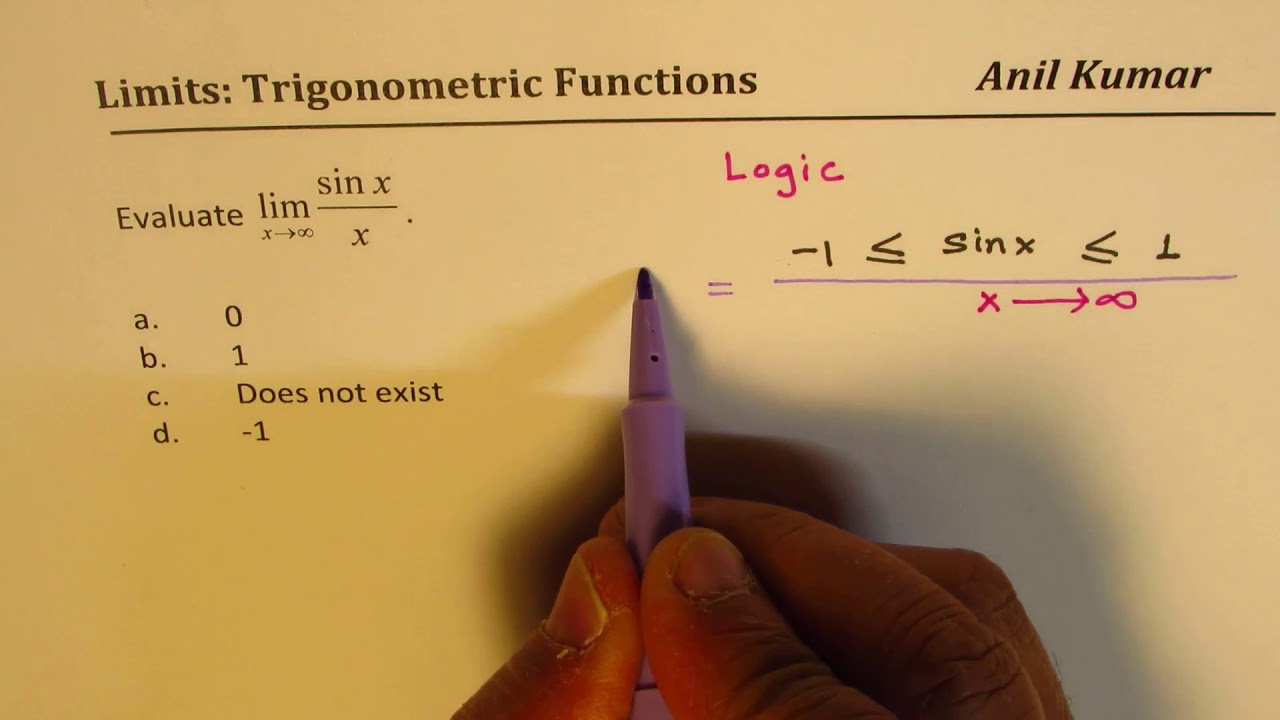



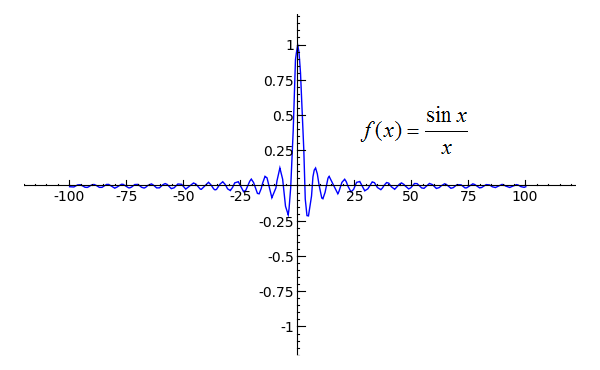
Evaluate Limit As X Approaches Infinity For Sinx Over X Youtube
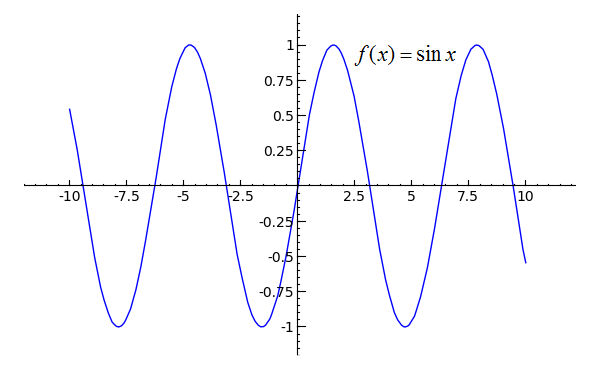



Sage Calculus Tutorial Limits At Infinity




Limit Of A Function Wikipedia



Finding Limits Graphically




Calculus How Is The Answer To Lim X Pi 2 Tan X Negative Infinity And Positive Infinity Quora



Does The Limit As X Approaches 0 Of The Function 1 X 2 Exist It S My Understanding That It Is Not Continuous But Both The Left And Right Hand Limits Approach Infinity Quora



1



Calculus Limits




Limits To Infinity
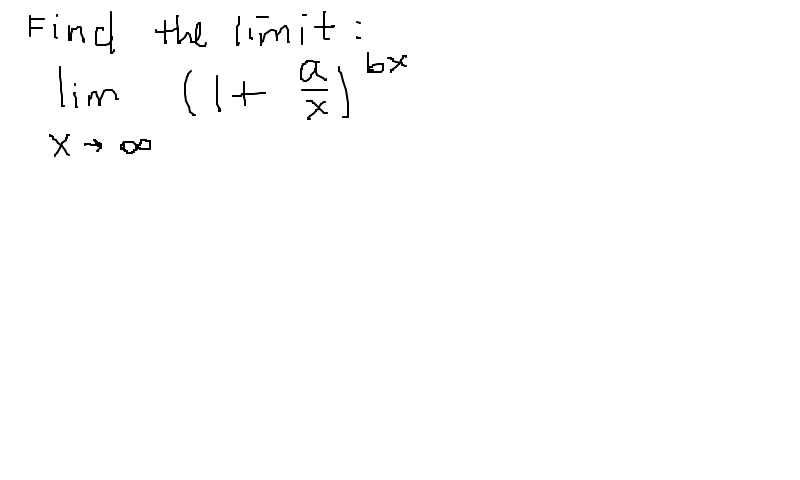



What Is The Limit As X Approaches Infinity Of 1 A X Bx Socratic




Solving Limits At Infinity Intuition And Examples
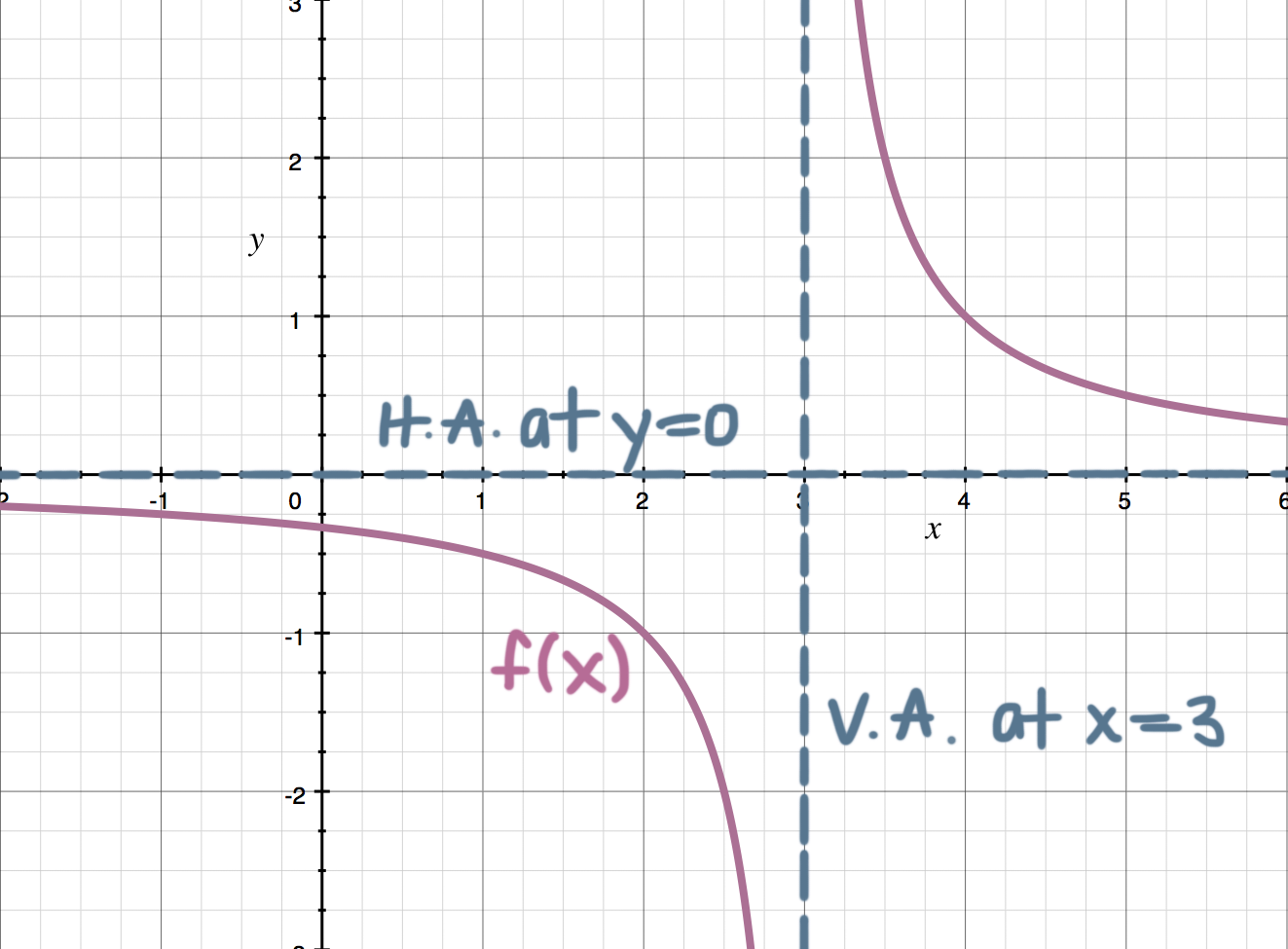



Limits At Infinity And Horizontal Asymptotes Krista King Math Online Math Tutor
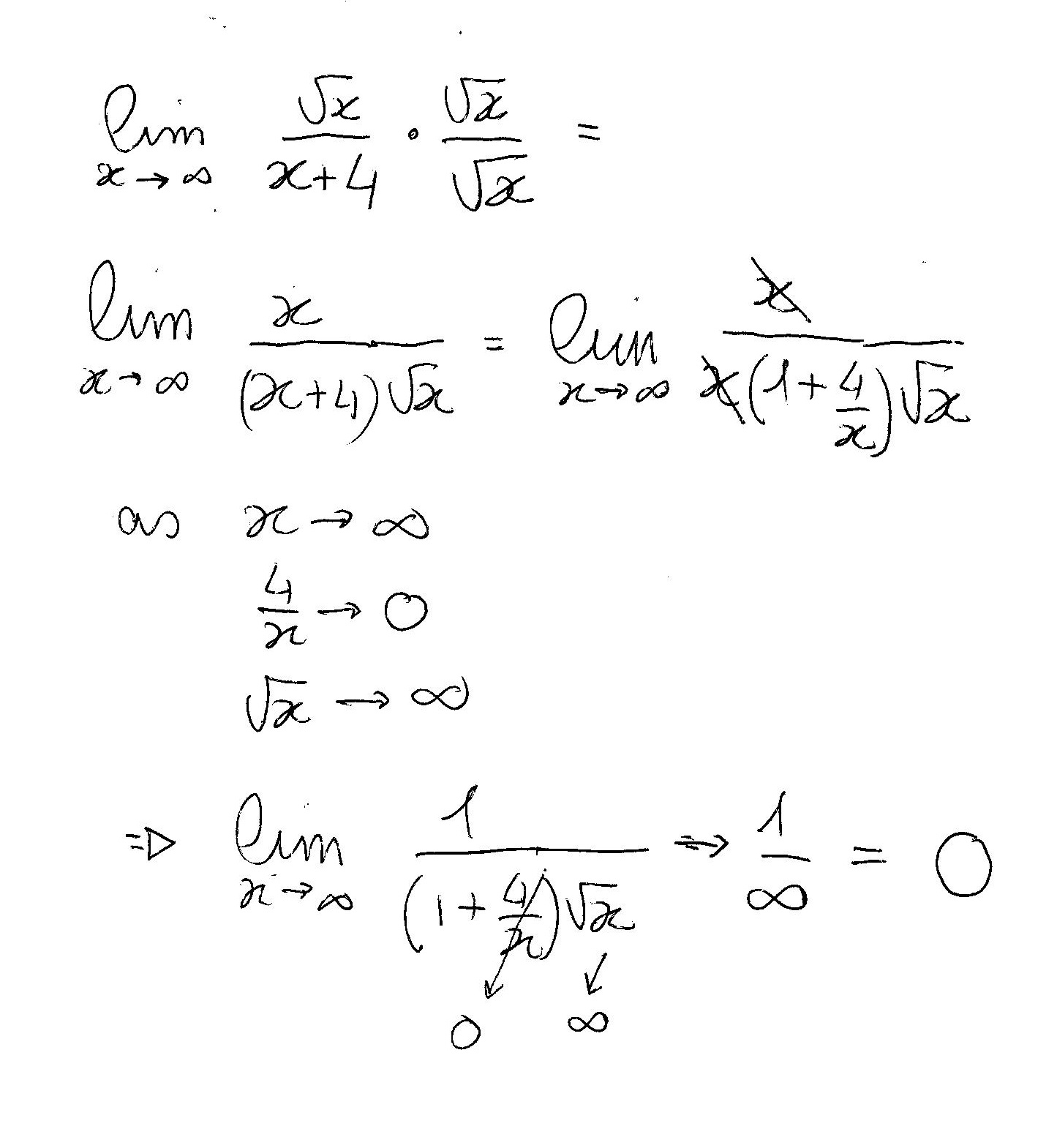



What Is The Limit Of Sqrt X X 4 As X Approaches Infinity Socratic



2 2 The Limit Of A Function Calculus Volume 1
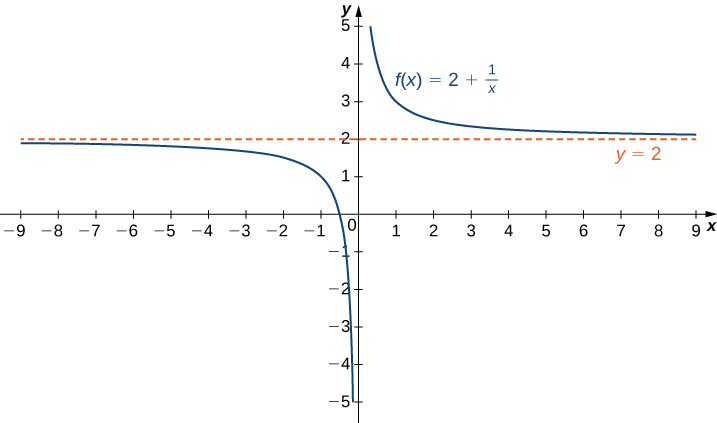



2 5 Limits At Infinity Mathematics Libretexts



0 件のコメント:
コメントを投稿